AtCoder Grand Contest 040
Updated:
Source codes
Solutions
A - ><
Solution
First, we initialize vector<ll> V(N, 0LL); as a candidate for good sequences. We divide this problems into two parts as follows.
- For all $i \in (N - 1)$ with $S[i] = “<”$, we change $a _ {i + 1}$ so that $a _ i < a _ {i + 1}$ in ascending order.
- For all $i \in (N - 1)$ with $S[i] = “>”$, we change $a _ {i}$ so that $a _ i > a _ {i + 1}$ in descending order.
This greedy algorithm works. We can solve this problem in $O(2N) = O(N)$-time.
B - Two Contests
Solution
We focus on $x = \mathop{\mathrm{argmin} } _ i R _ i$ and $y = \mathop{\mathrm{argmax} } _ i L _ i$. If $x = y$, or $x$ and $y$ are included in the same contest, in this contest the number of the satisfied people must be $\max(0, R _ x - L _ y)$. Thus the best strategy is that we choose $z = \mathop{\mathrm{argmax} } _ {i \in N \setminus \{ x, y \} } R _ i - L _ i$ and let the other contest consist of only one problem $z$. Let $ans _ 0$ be the answer by this case.
So we consider otherwise, that is, we consider, given $x \neq y$, the one contest $X$ includes $x$ and the other $Y$ includes $y$. Let’s see what is the best strategy here. Let $V = N \setminus \{ x, y \}$. and sort $I = \{ (L _ i, R _ i) \} _ {i \in V}$ in descending order of $R _ i$. We choose some ranges from $I$ to push into $Y$. What is the best strategy here?
Let’s focus on $r = \min _ {i \in B} R _ i$. To make the argument simple, we fix $r$. For $e = (L _ i , R _ i) \in I$, If $R _ i \geq r$, we should push $e$ into $B$ because if we push $e$ into $B$, we don’t lose anyone satisfied, but if we push $e$ into $A$, we may or may not lose those, which is not the best strategy. On the other hand, if $R _ i < r$, we must push $e$ into $A$; or otherwise it contradicts the definition of $r$. Therefore we conclude that our best strategy is that trying all $0 \leq k \leq N - 2$. We push $(L _ i, R _ i) \in I$ into $B$ if $i < k$ and into $A$ if $i \geq k$.
Let’s discuss the time complexity. Sorting $I = \{ (L _ i, R _ i) \} _ {i \in V}$ in descending order of $R _ i$ takes $O(N \log N)$-time. We can compute all $r _ k = \min _ {i < k} R _ i$ and $l _ k = \max _ {i \geq k} L _ i$ by partial min/max method in $O(N)$-time. The answer is \[ \max \left( ans _ 0, \max _ {0 \leq k \leq N - 2} \left( \max\left(0, R _ x - l _ k \right) + \max\left(0, r _ k - L _ y \right) \right) \right). \]
C - Neither AB nor BA
Solution
We translate $s$ into $S$ as follows.
\[
S[i] = \begin{cases}
s[i] & i \text{ is even}, \\
B & i \text{ is odd and } s[i] = A, \\
A & i \text{ is odd and } s[i] = B, \\
C & i \text{ is odd and } s[i] = C.
\end{cases}
\]
The map $s \mapsto S$ is a bijection. So we count the number of good $S$. In $S$, the forbidden pairs of characters are $AA$ and $BB$. Hereinafter, we use $A, B, C$ to denote the number of A, B, C in $S$, respectively.
The number of the manipulations must be $N / 2$. Thus we see that, if $A > N / 2$ or $B > N / 2$, we cannot reduce $S$ into the empty string. However, otherwise, we can reduce $S$ into the empty string. Why? Let’s consider the case where $A = B = N / 2$. Then, we can find a place where A and B are adjacent to each other. We eliminate it. Then the problem becomes smaller than the original problem. We can continue this manipulation $N / 2$ times. Other cases are almost the same. We regard each C as A or B virtually so that $A = B = N / 2$. Then the same strategy works.
Let $X$ be the number of $S$ that satisfies $A > N / 2$. The case $B > N / 2$ is the same. The answer is $3 ^ N - 2X$. Here, $X$ is computed as follows. \[ X = \sum _ {N / 2 + 1 \leq k \leq N} \begin{pmatrix} N \\ k \end{pmatrix} 2 ^ {N - k}. \]
D - Balance Beam
Observation
Let’s see this problem from the viewpoint of two graphs. Let the $x$-axis denote the time and the $y$-axis denote the distance from the starting point. We draw two graphs and let $I = \{ (A _ i, B _ i) \} _ {i \in N}$ be ordered as the following picture (from the official YouTube live).
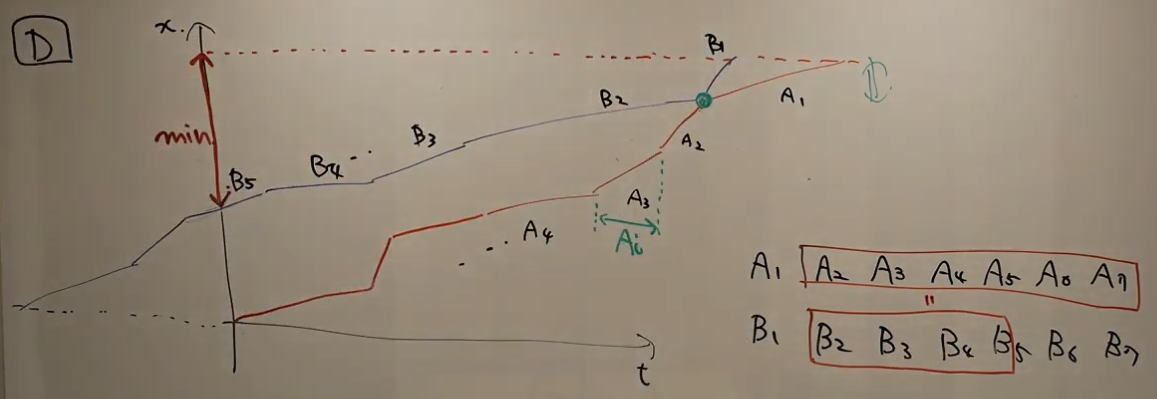
Then, the problem will be translated as follows.
Problem D.1: Rearrange $I$ to minimize $(M, r) \in N \times [0, 1)$ so that there exists $k \in N$ so that \[ \sum _ {i = k} ^{N - 1} A _ i \leq \sum _ {i = k} ^ {M - 1} B _ i + r B _ M. \tag{D.1} \]
Let $C _ i = \max(A _ i, B _ i)$. We will show that Problem D.1 is equivalent to the following problem.
Problem D.2: Rearrange $I$ to minimize $(M, r) \in N \times [0, 1)$ so that \[ \sum _ {i = 0} ^{N - 1} A _ i \leq \sum _ {i = 0} ^ {M - 1} C _ i + r B _ M. \tag{D.2} \]
Let $(M, r) \in N \times [0, 1)$ satisfy the constraints of Problem D.1. There exists $k \in N$ satisfying (D.1). Then, (D.2) immediately follows by the definition of $C _ i$. Next, let $(M, r) \in N \times [0, 1)$ satisfy the constraints of Problem D.2. We can rearrange the order of $I$ so that there exists $1 \leq k \leq N$ so that
\[
C _ i = \begin{cases} A _ i & i < k, \\
B _ i & i \geq k. \end{cases}
\]
Then, (D.2) becomes (D.1), which completes the proof.
Solution
We can solve Problem D.2 to try all $B _ i$ for $b = B _ M$. Fix $b = B _ M$. Then, the best strategy to minimize $M$ is that we choose $C _ i$ in the descending order. We can do this greedy algorithm in $O(\log N)$-time for each $b$ by binary search if we prepare partial sums in $O(N)$-time. Then, we compute $r$ as follows. \[ r = \max \left(0, \frac{\sum _ {i = 0} ^ {N - 1} A _ i - \sum _ {i = 0} ^ {M - 1} C _ i}{B _ M} \right). \] In this case, the answer is \[ \frac{N - M - r}{N}. \] We compute the maximum of them.
We have to care one type of corner cases. If we have
\[
\sum _ {i = 0}^ {N - 1} A _ i = \sum _ {i = 0}^ {N - 1} C _ i,
\]
the answer is 0 1. These cases are not necessarily corner cases if the implement is good, but be careful.
E - Prefix Suffix Addition
We use $a[i]$ instead of $A[i]$. I should have made correct pictures. We use $0$-indexed, but, without loss of generality, we insert $a[0] = 0$ and $a[N + 1] = 0$.
Preliminary
We are given two operations. But first of all, we consider only “Operation 1”. How many times we need to meet the objective? Of course we can construct arbitrary $\{ a[i] \}$ by $N$ times. Just make $a[i]$ for each manipulation. But we may or may not reduce the number of it. Let’s consider the following sequence.
\[ 0, 2, 1, 3, 4, 6, 5, 0. \]
Here we point out “$2, 1$”. We need at least a pair of operations to make this since $2 > 1$. We can find two more points: $6 > 5 > 0$. So we have to use the operation at least three times.
On the other hand, three times is suffice to make this sequence. We can construct as follows.
\[
\begin{align}
& 0, 2, \\
& 0, 0, 1, 3, 4, 6, \\
& 0, 0, 0, 0, 0, 0, 5.
\end{align}
\]
Generally speaking, we can show that, to obtain the sequence $\{ a[i] \}$, we need exactly $x$ operations, where $x$ is the number of $i$ with $a[i] > a[i + 1]$.
We can say the same thing for “Operation 2”. we need $y$ times, where $y$ is the count of “$<$”.
Translate the problem into another
By the observation above, we see that all we have to do is solve the following problem.
Problem E.1: We will split each $a[i]$ into two nonnegative integers $b[i]$ and $c[i]$ with $a[i] = b[i] + c[i]$. Find the minimum count of $i$ with $b[i] > b[i + 1]$ plus $i$ with $c[i] < c[i + 1]$.
We regard an “$i$ with $b[i] > b[i + 1]$” and an “$i$ with $c[i] < c[i + 1]$” as a penalty. We regard the number of the accumulated penalties as a distance.
It is natural for us to convert Problem E.1 into DP. Obviously, we can forget the details $j < i$ when considering $i \mapsto i + 1$. How much information do we need? Before estimating the time or memory complexity, we observe the transitions.
Details of DP
To say the conclusion first, we possess the states by vector<map<int, int>> M;.
$M[i][h] = $ the minimum distance between $0$ and $i$ with the height $b[i] = h$; $c[i] = a[i] - h$.
Initial State
We start by $M[0][0] = 0$; otherwise, $M[i] = \emptyset$.
Answer
The answer is $M[N + 1][0]$.
Transition
Here we promise if $M[i][k]$ is empty, we skip it of course. In addition, we regard $M[i + 1][k] = \infty$ if it is empty.
For $i = 0, \dots, N$, for $(h, d) \in M[i]$, we have two types of transitions; the case $a[i] \leq a[i + 1]$ and the case $a[i] \geq a[i + 1]$.
For both cases, we will split $a[i + 1] = b[i + 1] + c[i + 1]$; $h’ = b[i + 1]$. Remember that if $h > h’$, we have $1$ penalty; if $a[i] - h < a[i + 1] - h’$, we have $1$ penalty. So we see that $h’$ should be the lowest as long as we have the same distance. Just memorizing the lowest height is suffice.
Let’s see the former case $a[i] \leq a[i + 1]$, which is the easier case.
\[
\begin{align}
M[i + 1][a[i + 1] - (a[i] - h)] & \gets \min(M[i + 1][a[i + 1] - (a[i] - h)], d), \\
M[i + 1][h] & \gets \min(M[i + 1][h], d + 1), \\
M[i + 1][0] & \gets \min(M[i + 1][0], d + 2).
\end{align}
\]
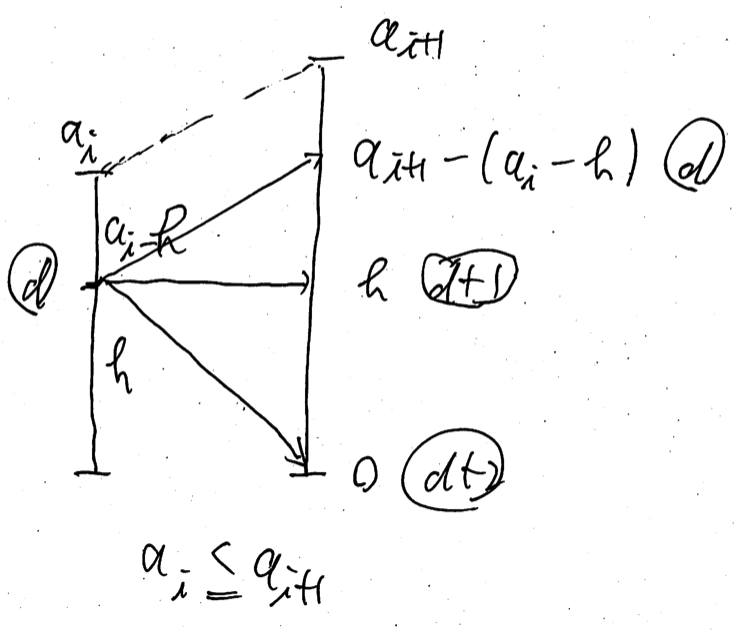
The latter case $a[i] \geq a[i + 1]$ is a little bit complicated.
\[
\begin{align}
M[i + 1][h] & \gets \min(M[i + 1][h], d) & & \text{ if } h \leq a[i + 1], \\
M[i + 1][k] & \gets \min(M[i + 1][k], d + 1) & & \text{ where } k = \max(0, a[i + 1] - (a[i] - h)), \\
M[i + 1][0] & \gets \min(M[i + 1][0], d + 2). & &
\end{align}
\]
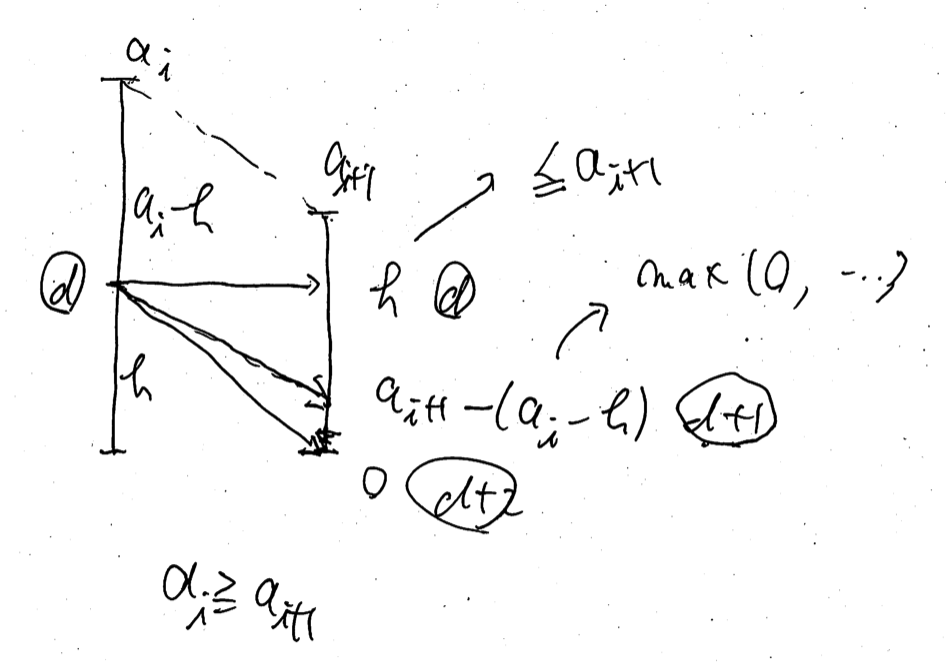
After the all transitions for $M[i] \mapsto M[i + 1]$, we erase unneeded elements on $M[i + 1]$. We consider $(h, d) \in M[i + 1]$ in the ascending order. If we find a pair $\{ (h, d), (h’, d’) \}$ with $h \leq h’$ and $d \geq d’$, we can erase $(h’, d’)$ since $(h, d)$ is a better state than it.
Time complexity
Now we can show the following lemma.
Lemma E.2: For each $i$, $M[i]$ has at most three elements: \[ M[i] = \{ (0, d + 2), (h _ 1, d + 1), (h _ 2, d) \}, \tag{E.1} \] with $0 \leq h _ 1 \leq h _ 2 \leq A[i]$.
Proof: We show this lemma by mathematical induction on $i$. If $i = 0$, it is done immediately. Suppose the case $i$ is true. From $(h _ 2, d) \in M[i]$ in (E.1), we create $(0, d + 2) \in M[i + 1]$. we cannot create $(h’, d’)$ with $d’ < d$ by the transition rule and our current assumption. Then, after erasing, we have at most three elements in $M[i + 1]$ where $d$, $d + 1$ and $d + 2$ as its second value, which completes the proof.
So each transition takes $O(1)$-time. The total time complexity is $O(N)$.
F - Two Pieces
Preliminary
First, here we promise that the two pieces are indistinguishable and the two manipulation for $(x, x + 1) \to (x + 1, x + 1)$ are indistinguishable, too.
Instead of considering $(A, B)$ with $A \leq B$, we consider the pair of nonnegative integers $(x, d)$ where $x = B$ and $d = B - A$. Then, there are three manipulations here.
- $x \mathbin{ {+} {+} }$; $d \mathbin{ {+} {+} }$;
- $d \mathbin{ {-} {-} }$; only when $d \geq 2$.
- $d = 0$;
They are distinguishable because we have restricted the manipulation 2. when $d \geq 2$. We use $X, Y, Z$ to denote the number of the manipulations of 1., 2., 3., respectively. We immediately see that $X + Y + Z = N$ and $X = B$.
Observation
Let’s consider the transition of $d$ without the manipulation 3. We fix $Y$, which runs $0 \leq Y \leq \min(A, N - B, B - 1)$. We have to make these $X + Y$ elements in a good order, whose number is equal to $\mathrm{Catalan}(X - 1, Y)$, so as not to break the condition for the manipulation 2., that is, $d \geq 2$. We draw a picture of the transition of $d$ as below. Let $D$ be the resulting $d$, that is, $D = B - A$. The final height of $d$ in the picture is equal to $X - Y$.
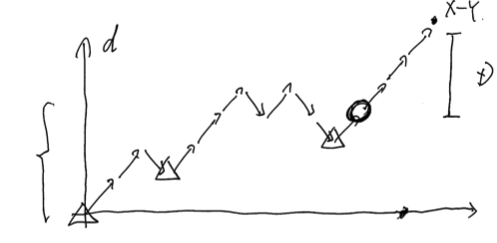
Then, where can we insert the manipulations 3? The number of those is $Z$. First, we must insert at least one element into the final point where the height of $d$ is equal to $X - Y - D$ to make the resulting $d$ is equal to $D$. Why must it be final? Because otherwise we will break the rule of $d \geq 2$ for the manipulation 3. Second, we may insert any elements into the final point where the height of $d$ is less than or equal to $X - Y - D$. Why it must be final is the same before.
Therefore, what we have to do is divide $Z - 1$ elements into $X - Y - D + 1$ parts. The count of that possible division is as follows. \[ \begin{pmatrix} (X - Y - D + 1) + (Z - 1) - 1 \\\ (X - Y - D + 1) - 1 \end{pmatrix}. \tag{F.1} \] Here, we promise that out of range is $0$.
Corner Cases
We have to be careful for two types of the corner cases.
One is simple. If $A = B = 0$, we just flush $1$ instead of $0$.
The other is rather difficult. Consider what happens given $Z = 0$. In normal cases, the count is $0$ because we need at least one element to adjust the resulting $d$. But if $X - Y = D$, we don’t need any element for manipulation 3. So in this case, instead of (F.1) being $0$, we use $1$.
