AtCoder Grand Contest 036

AtCoder Grand Contest 036

Source codes

• My submissions (AtCoder)
• My source codes (GitHub)

Solutions

A - Triangle

前提

最初の点を $(0, 0)$ に設定するのは当たり前だと思う。すると次式を成立させる $x _ 0$, $y _ 0$, $x _ 1$, $y _ 1$ を構成するのが目的である。 \[ x _ 0 y _ 1 - x _ 1 y _ 0 = S. \tag{A.1} \] ただし $1 \leq S \leq 10^{18}$ に対し、他の変数は $0$ 以上 $10^9$ 以下のみ許される。

模範解答

$x _ 0 = 10^9$ とする。 $x _ 1 = 1$ とする。すると $y _ 1 = (S + C - 1)/C$ とすれば、 $x _ 1$ は正しく求まる。

ポイント

私の解法は正しくなかった。嘘解法で通してすみません。

B - Do Not Duplicate

模範解答

$0$-indexed とする。 stack が $\emptyset$ になるのは、一番下に埋め込まれた数字が取り出される瞬間である。つまり、最初に現れた数字が再度出てくる時である。このひとまとめをブロックと呼ぶことにする。例えば \[ [1, 2, 3, 2, 3, 1], [2, 3, 2], [3, 1, 2, 3], \dots \] のようにする。

$a[0][i] = A[i]$ の数字を先頭とするブロックの要素数

と定める。すると $(i + a[0][i]) \% N$ は次のブロックの先頭を指している。これがポイント。そこで doubling をすることにする。

$a[k][i] = A[i]$ の数字を先頭とする $2^k$ 個のブロックの要素総数

と定める。するとこれは次式で求まる。 $k = 1, 2, \dots, 59$ に対し、 $i = 0, \dots, N - 1$ に対し、 \[ a[k][i] = a[k - 1][i] + a[k - 1][(i + a[k - 1][i]) \% N]. \]

あとは限界ギリギリまで登っていき、進むのを繰り返す。「最後のブロック」の先頭を $start$ とすると、ここから先はシミュレーションをすれば答えが求まる。例えば deque<int> D; と vector<bool> stacked(200010, false); を用いる。

ポイント

本番では周期を用いて求めたが、実装するうちにダブリングの方が普通だと思うようになってきた。

C - GP 2

私の解答

まず $3M$ ポイントを $N$ 人でただただ山分けをする場合の数は \[ ans = \begin{pmatrix} 3M + N - 1 \\\ N - 1 \end{pmatrix} \] である。ここから GP 2 のルールでは「ありえない」分布を引くことにする。次の 2 パターンがある。

点数取りすぎ

全部優勝しても $2M$ ポイントしか獲得できない。そのため、 $2M + 1$ ポイント以上を獲得している人がいる分布は全てアウトである。

このような人は $1$ 人しかいない。この人をまず選んで、あとは山分けしたものがこれに該当する。つまり $K = 2M + 1, \dots, 3M$ に対し、 \[ ans \mathbin{ {-} {=} } N \begin{pmatrix} 3M - K + N - 2 \\\ N - 2 \end{pmatrix} \] とする。

優勝者がいない

「 $2$ ポイントを獲得した」という事象がどう頑張っても $M - 1$ 回数以下しか観測できない分布は弾くしかない。それはつまりどういうことかというと、 $K = 0, 1, \dots, M - 1$ に対し、まず $K$ 束の $2$ ポイントを山分けした分布 $X$ と、 $0, 1$ 列からなる合計ポイント $3M - 2K$ を獲得した分布 $Y$ を足したものである。後者は、わかりやすくいうと $N$ 人のうちから $3M - 2K$ 人を選んでその人たちに $1$ ポイントずつ渡すということである。 $X, Y$ は完全に独立なので $X + Y$ の場合の数は積、つまり次式で取り除くことができる。 \[ ans \mathbin{ {-} {=} } \begin{pmatrix} K + N - 1 \\\ N - 1 \end{pmatrix} \begin{pmatrix} N \\\ 3M - 2N \end{pmatrix}. \]

これで答えが求まる。

解法の正当化

$0$-indexed とする。 $i \in N$ 番目の人が $a _ i$ 回優勝し、 $b _ i$ 回準優勝したとする。すると分布 $\{ x _ i \}$ には \[ x _ i = 2a _ i + b _ i \text{ for any } i \in N \tag{C.1} \] という制約がかかり、さらに次の制約がかかる。 \[ \sum _ {i \in N} a _ i = \sum _ {i \in N} b _ i = M. \tag{C.2} \] もう一つ、優勝者と準優勝者が毎回異なる必要がある。つまり、次の制約がかかる。 \[ a _ i + b _ i \leq M \text{ for any } i \in N. \tag{C.3} \]

私たちが今判定したいのは、与えられた分布 $\{ x _ i \}$ に対して、上記の条件を充たす非負整数のペアの列 $\{ (a _ i, b _ i) \} _ i$ が存在するかどうかということである。

与えられた分布 $\{ x _ i \}$ は、上で議論した条件を充たすものとする。すなわち、 \[ \begin{align} \sum _ {i \in N} x _ i &= 3M, \tag{X.1} \\
x _ i &\leq 2M \text{ for any } i \in N, \tag{X.2} \\
\sum _ {i \in N} \left( x _ i \% 2 \right) &\leq M \tag{X.3} \end{align} \] であるとする。そこで一旦まず、 \[ a _ i = x _ i / 2, \ b _ i = x _ i \% 2 \text{ for any } i \in N \tag{C.4} \] とすると、 (C.1) は充たされる。また、(X.2) から (C.3) も充たされる。 (X.3) により、今のところ \[ \sum _ {i \in N} b _ i \leq M \tag{C.2’} \] も充たされている。あとは (C.2) を充たすように (C.3) の余裕のあるところから $a _ i$ を $1$ 減らして $b _ i$ を $2$ 増やすことをすればよろしい。 (C.2’) の等号が成立するとき、 (X.1) より (C.2) が成立することになる。

ポイント

これは直感と実装の両方で良い戦いができた。

D - Negative Cycle

負閉路がない・ポテンシャル

グラフのポテンシャルを定義する。

定義 D.1： $G = (V, E)$ を重み付き有向グラフとする。 $p \colon V \to \mathbb{Z}$ が $G$ の ポテンシャル であるとは、 $(x, y, c) \in E$ に対し、 \[ p _ y \leq p _ x + c \tag{D.1} \] が成立することをいう。

ポテンシャルと負閉路について、以下が知られる。

定理 D.2： $G = (V, E)$ を重み付き有向グラフとする。 $G$ に負閉路がないことは、 $G$ のポテンシャル $p \colon V \to \mathbb{Z}$ が存在することと同値である。

証明の概略：ポテンシャルが存在するときに、負閉路が存在しない理由は簡単である。 (D.1) を変形すると \[ p _ y - p _ x \leq c \] が得られるが、これを閉路を構成する全ての辺について足すと、和が $0$ 以上であることが従う。したがって全ての閉路は非負である。負閉路が存在しないときにポテンシャルが定義できるのは、適当に最小値をとったりすればいいらしい。またこれにより、 $p$ の値域は $\mathbb{Z}$ だけ考えれば十分であることも従う。

今回の問題は、負閉路が存在しない条件を考察するのだから、適当な $p$ を決め打ちして、 それがポテンシャルとなるためにあってはならない辺を取り除く という段取りでいく。

今回のポテンシャルの条件

$1$-indexed とする。まず $(i, i + 1, 0)$ が削除できないということは、 $p$ は広義単調減少であるということである。そこで、 $p$ を直接捉えるのではなく、区切りで捉えることにする。下図のように。

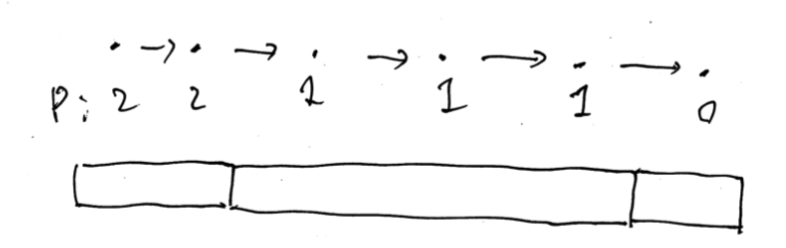
このときの違反辺は以下の通り。

• $x < y$ なる $(x, y, -1)$ について：この場合は同じブロック同士の辺を全て消す必要がある。
• $x > y$ なる $(x, y, 1)$ について：この場合は今見ているブロックの点から $2$ つ以上前のブロックの点への辺を全て消す必要がある。

つまり $2$ つ前のブロックまで覚えておけば十分である。つまり DP の keys は $2$ 個で $1$ つの遷移に $O(N)$ かけて計算する。

DP の遷移

$dp[i][j] = j$ まで見たとき、直前の仕切りが $i$ だった時の最小コスト(下図参照)。

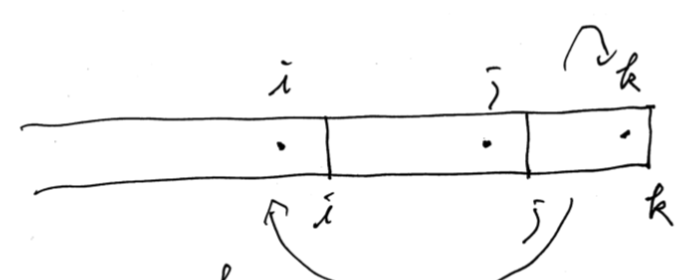
初期状態： $dp[0][0] = 0$, otherwise $\infty$. 答え： $\min _ {0 \leq i < N} dp[i][N]$. 遷移： $dp[i][j] \mapsto dp[j][k]$ と遷移することにする。 $j = 0, \dots, N - 1$ に対し、 $i = 0, \dots, j$ に対し、 $dp[i][j] = \infty$ なら continue, そうでないなら $k = j + 1, \dots, N$ に対し、 \[ dp[j][k] \gets \min \left( dp[j][k], dp[i][j] + \sum _ {x = j + 1} ^ k \sum _ {y = j + 1} ^ {x - 1} A _ {y, x} + \sum _ {x = j + 1} ^ k \sum _ {y = 1} ^ i A _ {x, y} \right). \tag{D.2} \] ここで $\sum$ の和を真面目に計算するわけにいかないが、簡単に order を落とせる。 \[ \begin{align} sum0[j][x] &= \sum _ {y = j + 1} ^ {x - 1} A _ {y, x}, \\
sum1[i][x] &= \sum _ {y = 1} ^ i A _ {x, y} \end{align} \] とする。この問題は $O(N ^ 3)$ が許されるので愚直に前計算して構わない。あとは $k$ の loop に入る前に $tmp0 = tmp1 = 0$ としておき、 $k$ のループで次式を実行すれば (D.2) 式が達成される。 \[ \begin{align} tmp0 & \mathbin{ {+} {=} } sum0[j][k], \\
tmp1 & \mathbin{ {+} {=} } sum1[i][k], \\
dp[j][k] & \gets \min \left( dp[j][k], dp[i][j] + tmp0 + tmp1 \right). \end{align} \] 計算量は $O(N^3)$ である。

ポイント

わかってしまえばただの DP なのだが、自力で解くことはできないだろう。学ぶことは多い。

E - ABC String

初期的考察

まず同じ文字は連続して選べないので、最初から圧縮して良い。また、必要なら文字を入れ替えることにより $\sharp A \leq \sharp B \leq \sharp C$ を仮定して良い。

答えの文字を構築するために、次の命題が有効である。

命題 E.1： $\sharp A \leq \sharp B = \sharp C$ のとき、 $A, B, C$ たちを $\sharp A$ 個取れる。

証明：まず $A$ の出てくるところで split することにする。つまり、 \[ (BC - str) A (BC - str) A \dots A (BC - str) \] とする。ここで $BC - str$ は $B$ と $C$ を交互に続けた文字列である。空文字列を許す。これを順番に vector<string> V に突っ込むものとする。このサイズを $N = \sharp A + 1$ とする。ここで 3 段階に渡って $B, C$ を選ぶことにする。

1. $i = 0, \dots, N - 1$ に対し、 $\lvert V[i] \rvert$ が奇数ならば、先頭の文字を選ぶ。
   • これにより選ばれる $B, C$ の数は等しい。なぜなら $\sharp B = \sharp C$ であり、選ばれなかった文字は $BC$ or $CB$ を連続させたものであるから同数である。ゆえに余りも同数である。
   • これにより選ばれる $B, C$ の数は $\sharp A$ を超えない。なぜなら超えた場合それは $N$ であるが、この時 $\sharp B = \sharp C$ が成り立たない。
2. $i = 1, \dots, N - 2$ に対し、 $\lvert V[i] \rvert$ が偶数ならば、先頭の $2$ 文字を選ぶ。
   • これにより選ばれる $B, C$ の数は等しい。上の考察から自明。
   • これにより選ばれる $B, C$ の数は $\sharp A$ を超えない。上とほぼ同じ議論による。
3. ここまでで $B, C$ の選んだ数が $\sharp A$ 未満の場合、 $\sharp A$ 個になるまで、今まで選んでいない $BC$ or $CB$ を好きに選ぶ。

これは条件を充している。また $\sharp A$ 個を超えて選ぶことはできないので、これが最善であることもわかる。構築方法も与えている。

命題 E.1 に帰着させる

そこで問題になるのは $\sharp A \leq \sharp B < \sharp C$ の場合である。このとき、まず $C$ を取り除けるだけ取り除いて $\sharp A \leq \sharp B = \sharp C$ を達成させられば上の命題に帰着する。犠牲なく取り除ける $C$ は以下の 2 通り。

• 先頭または末尾の $C$,
• $ACB$, $BCA$ の $C$.

これを全て取り除いても $\sharp A \leq \sharp B < \sharp C$ である場合もある。この場合は文字列の形が限定されている。具体的には以下のようになっている。 \[ [ACACA][BCB][ACA][BCBCBCB] \tag{E.1} \] この例だと $(\sharp A, \sharp B, \sharp C) = (5, 6, 7)$ である。そこでもはや $A$ を犠牲にして $C$ を消去する以外に方法がない。すると $AC$ を見つけて消去することになる。つまり、 \[ [ACA][BCB][ACA][BCBCBCB] \tag{E.2} \] となる。この例だと $(\sharp A, \sharp B, \sharp C) = (4, 6, 6)$ である。命題 E.1 を使うことができる。

最善である理由

上の $[ ]$ をブロックと呼ぶことにする。ブロックの個数を $k$ とする。

補題 E.2： (E.1) を (E.2) に変換したあと、 $\sharp A = k$ が成立する。

証明：変換において、常に $\sharp C = \sharp A + \sharp B - k$ が成立する。 (E.2) に変換すると $\sharp B = \sharp C$ が成立する。よって $\sharp A = k$ となる。

補題 E.3： (E.1) から選ぶことのできる $A, B, C$ の個数は $k$ 個以下である。

選ぶ $A, B, C$ の個数を $a, b, c$ とかく。各ブロックに対し $(A or B)C$ が交互に並んでいるため $a + b - c \leq 1$ が成立する。これを $k$ 個のブロックについて和をとると $a + b - c \leq k$ が成立する。最終結果は $a = b = c$ なので、 $a = b = c \leq k$ が成立する。

ポイント

実装は大変だった。上の流れをそのままプログラムにすると以下の通りになる。

int main()
{
  string S;
  cin >> S;
  S = reduce(S); // 連続した文字を圧縮する
  map<char, char> M, R;
  M = make_map(S);
  R = make_rev(M);
  S = convert(S, M); // \sharp A \leq \sharp B \leq \sharp C が成立するように変換
  vector<int> cnt = count(S);
  if (cnt[1] < cnt[2]) // \sharp B < \sharp C なら
  {
    S = erase_C(S); // 犠牲なく取り除ける C を出来るだけ取り除く
    cnt = count(S);
    if (cnt[1] < cnt[2]) // それでも \sharp B < \sharp C なら
    {
      S = erase_AC(S); // A を犠牲に C を取り除く
    }
  }
  string ans{make_ans(S)};
  ans = convert(ans, R); // 逆変換
  cout << ans << endl;
}

実装で間違えた箇所は以下の通り。

• 文字列を連結するときは stringstream を使うべきだが、文字列を走るときは string で良い。
• stringstream SS; の文字列を空にするときは SS.str({}); とする。 void stringstream::clear(); ではない。
• make_ans の中で split するときには、最後までやる。
• unsigned int i で i - 1 を書くのは危ない。 int を使うか、 i >= 1 の形で条件分岐をする。

F - Square Constraints

もし下の制約がなければ…

とても簡単である。選べる数字の個数を 昇順 に並べたものを $a _ 0, a _ 1, \dots, a _ {2N - 1}$ とすると、求める場合の数は \[ a _ 0 (a _ 1 - 1) \dots (a _ {2 N - 1} - (2 N - 1)) \tag{F.1} \] である。これを基礎として考察を進める。

本論

この問題は選んではいけないエリアが存在する。そこでその個数を含めて、図のように $\{ a _ i \}$, $\{ b _ i \}$, $\{ c _ i \}$ を定める( $i \in N$ )。

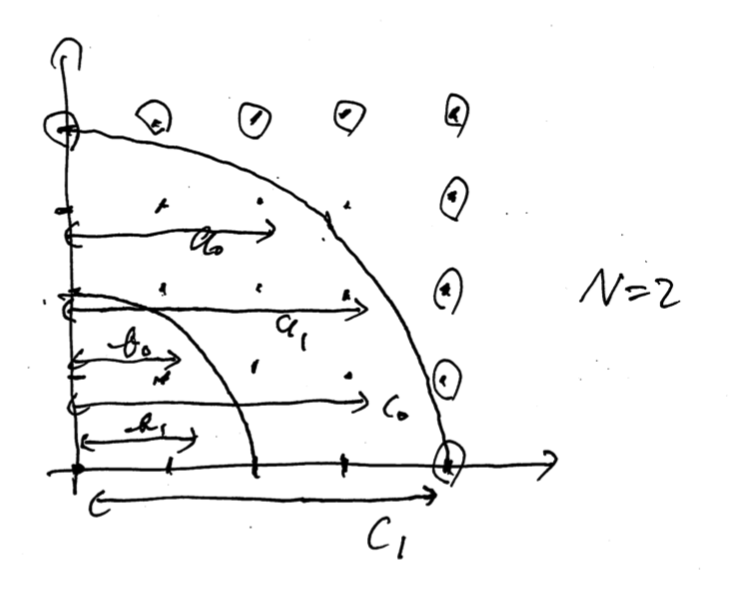
つまり、

$a _ i = $ 上から $i$ 番目の選んでいいものの個数、
$b _ i = $ 上から $i + N$ 番目の選んでいけないものの個数、
$c _ i = $ 上から $i + N$ 番目の選んでいいものといけないものの個数の和

と定める。これらを value の昇順に並べるのがポイントであるが、昇順で並べる(vector<Element> V; に入れるとする)と、

• 最初の $2N$ 個は $\{ a _ i \}$, $\{ b _ i \}$ が mixed している。ただし $\{ a _ i \}$ だけ、または、 $\{ b _ i \}$ だけ見たとき、 index が昇順に並ぶようにできる(きちんとタイブレークしておく)。
• 最後の $N$ 個は $\{ c _ i \}$ がそのまま並んでいる。

となっている。

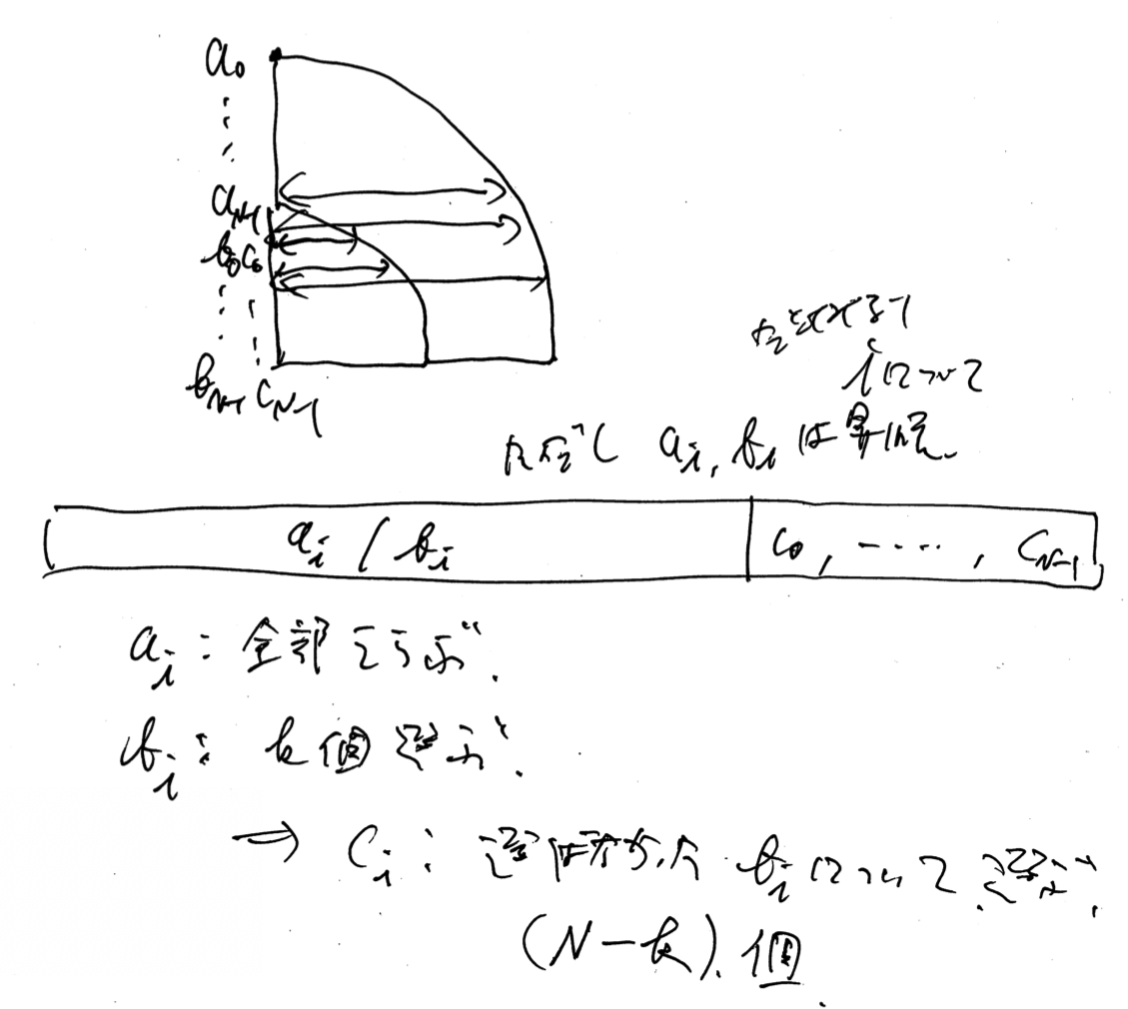
包除原理を使用する。 $\{ b _ i \}$ のうち、 選ぶものを $k$ 個と fix する 。すると $\{ c _ i \}$ は、 $b _ j$ で選ばなかった index $j$ に対し、 $c _ j$ は必ず選ぶことになる。これらが $(N - k)$ 個ある。

あとは前から $x$ 個見ていって $y$ 個選ぶ時の (F.1) の値を覚えておけばよろしい。ここで重要なことは、 $b _ j$ を見た時に「選ばない」場合は、 $c _ j$ をこの時点で「選ぶ」ことにする。このとき $c _ j$ から引くべき数は、前の elements の個数だけであるが、その個数は、

• $\{ a _ i \}$： 全部選ぶので $N$ 個、
• $\{ b _ i \}$： 規約により $k$ 個、
• $\{ c _ i \}$： 今まで選ばなかった $\{ b _ i \}$ の個数、つまり $(j - y)$ 個

により、 $(c _ j - N - k - (j - y))$ を掛け算すればいいとわかる。ここで $k$ を fix した効果が出ている。

DP に落とし込む

$0 \leq k \leq N$ を fix しておく。

$dp[x][y] = $ 前から $x$ 個を見ている。 $\{ b _ i \}$ を $y$ 個選んでいる。ここまでで構築される (F.1) の値。

と定める。初期状態： $dp[0][0] = 1$, otherwise $0$. 答え： $dp[2N][k]$ (というかこの値以外に有効な意味は全くない)。遷移： $x = 0, \dots, 2N - 1$ に対し、 $y = 0, \dots, x$ に対し、 $V[x].is\_a$ の場合、 \[ dp[x + 1][y] \mathbin{ {+} {=} } dp[x][y] \times (V[x].val - V[x].ind\_a - y). \] 一方で $!V[x].is\_a$ の場合、 \[ \begin{align} dp[x + 1][y + 1] &\mathbin{ {+} {=} } dp[x][y] \times (V[x].val - V[x].ind\_a - y), \\
dp[x + 1][y] &\mathbin{ {+} {=} } dp[x][y] \times (V[x].c - N - k - (V[x].ind - y)). \end{align} \]

あとは「答え」を $(-1) ^ k$ 倍して総和する。

実装について

struct Element
{
  mint val;
  mint c; // !is_a の場合に c_ind の値を入れておく
  int ind;
  int ind_a; // 今まで選んできた a の個数の情報を持っておく
  bool is_a;

  bool operator<(Element const &l) const
  {
    if (val == l.val)
    {
      return ind < l.ind; // タイブレークしておく
    }
    return val < l.val;
  }
};

$a, b, c$ の求め方は意外と厄介である。

vector<Element> make_elements(ll N)
{
  vector<Element> res(2 * N);
  // make_A
  for (auto i = 0LL; i < N; i++)
  {
    ll X = sqrt(4 * N * N - (i + N) * (i + N)) + epsilon; // 整数値の場合は切り上げる。
    res[i] = Element(N - 1 - i, min(2 * N, X + 1));
  }
  // make_B
  for (auto i = 0LL; i < N; i++)
  {
    ll X = sqrt(4 * N * N - i * i) + epsilon;
    ll Y = sqrt(N * N - i * i) - epsilon; // ここは整数値の場合は切り捨てる必要がある。
    res[i + N] = Element(N - 1 - i, Y + 1, min(2 * N, X + 1)); // 2N 個以上は取れない。要注意。
  }
  sort(res.begin(), res.end());
  // calc ind_a, 途中略
  return res;
}

ポイント

考察は難しいが、自然であり、しかも実装もそこまで難しくない。

Others