AtCoder Beginner Contest 135
Updated:
- Review: 2020-05-20, 21, 22.
Source codes
Solutions
A - Harmony
$K = (A + B) / 2$ とするしかない。計算機の割り算をする。 $\lvert A - K \rvert = \lvert B - K \rvert$ かどうかを判定する。
B - 0 or 1 Swap
$0$-indexed とする。 $\sharp \{ i \in \mathbb{N} \mid A _ i = i \} = 0, 2$ が条件である。
C - City Savers
前の方から貪欲に倒すのが最善である。
D - Digits Parade
DP による。 $M = 13$, $K = 5$ とする。 $S$ を reverse しておく。
$DP[i][j] = S$ の $i$ 文字目までみて $M$ で割ったときの余りが $j$ である場合の数
と定める。初期状態: $DP[0][0] = 1$, otherwise $0$. 答え $DP[S.size()][K]$. 遷移: $i = 0, \dots, S.size() - 1$ に対し、 $S[i] = ?$ の場合、 $j = 0, \dots, M - 1$ に対し、 $k = 0, \dots, 9$ に対し、 \[ DP[i + 1][(j + 10^i k) \% M] \mathbin{ {+} {=} } DP[i][j], \] その他の場合は、 $j = 0, \dots, M - 1$ に対し、 $k = S[i]$ とすると、 \[ DP[i + 1][(j + 10^i k) \% M] \mathbin{ {+} {=} } DP[i][j]. \]
E - Golf
Preliminary
We solve this problem by recursive way. We ask $f(x, y)$ the next step for each shot. Here, $f(x, y)$ returns an example of one valid shot from $(0, 0)$ aiming at $(x, y) \neq (0, 0)$.
Let $L = \lvert x \rvert + \lvert y \rvert$. Considering the parity, if $K$ is even and $L$ is odd, the answer is -1. Hereinafter, we exclude this case. In addition, we can assume the followings.
- If $x < 0$, we calculate $f(x, y) = (-X, Y)$ where $(X, Y) = f(-x, y)$.
- If $y < 0$, we calculate $f(x, y) = (X, -Y)$ where $(X, Y) = f(x, -y)$.
Therefore, we can assume $x \geq 0$ and $y \geq 0$. Moreover, we can see the following property, too.
- If $x < y$, we calculate $f(x, y) = (Y, X)$ where $(X, Y) = f(y, x)$.
Hence, hereinafter, we assume that $0 \leq y \leq x$ and ($K$ is odd or $L$ is even), and we are going to find one of the best strategies, i.e., to construct $f(x, y)$.
Observation
Lemma E.1: If $L > 2K$, one of the best strategies is just to get close to $(x, y)$. That is $f(x, y) = (t, K - t)$ where $t = \min(K, x)$.
Proof. This lemma is a direct consequence of the following proposition.
Proposition E.2: If $L \leq 2K$, we can reach $(x, y)$ by no more than $3$ shots. In addition, the followings holds.
(a) The number of the shots is $1$ if and only if $L = K$.
(b) The number of the shots is $3$ if and only if $L \neq K$, $L$ is odd and $K$ is odd.
(c) Otherwise, the number of the shots is $2$.
Given that this proposition is true, we show the lemma as follows.
The total number of the best shots will be no more than $L / K$. If $L \% K = 0$, The lemma is true by (a). Otherwise, the possible lower bound is $L / K + 1$ and it actually attains by the strategy combining the lemma and (c) if $L \neq K$ and the parity is valid. Otherwise, we need one more shot and this is realized by (b). This completes the proof.
Let’s show Proposition E.2. Here, (a) is obvious. Therefore, we assume $L \neq K$. To show (c), we notice that if the assumption of (b) fails, $L$ is even.
Lemma E.3: Assume that $L \leq 2K$, $L \neq K$ and $L$ is even. Then, one of the best strategies is to go to $(x - L/2, y + K - L/2)$.
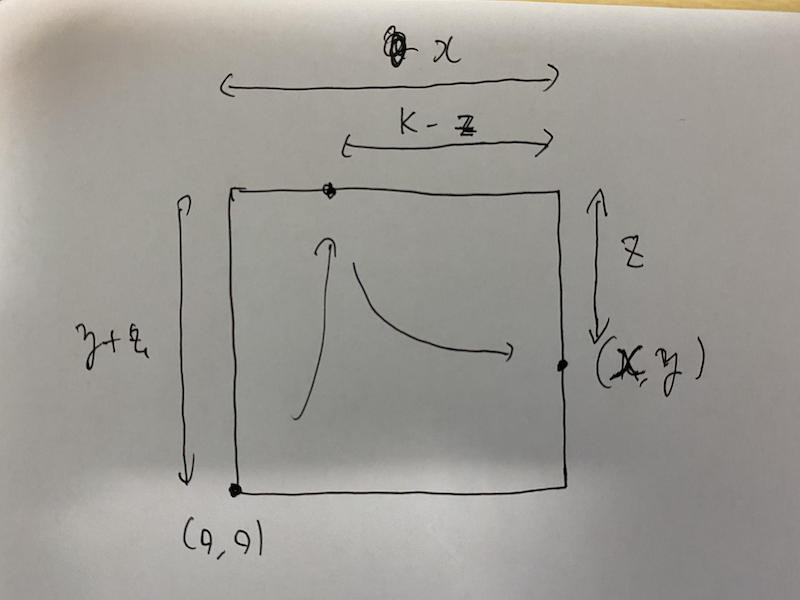
Proof. Let $z \geq 0$ be defined as the image above. We would like to demonstrate two shots as the arrows of the image show. Considering the total length of $2$ steps, we have $(y + z) + x + z = 2K$, i.e., $z = K - L/2$. Then, we go to $(x - (K - z), y + z)$. By direct calculation, we have the conclusion.
Lemma E.4: Assume that $L \leq 2K$, $L \neq K$, $L$ is odd and $K$ is odd. Then, one of the best strategies is just to get close to $(x, y)$.
Proof. As discussed above, in this case, we need at least $3$ shots to reach $(x, y)$. If we keep $L \leq 2K$ after the next shot, $L$ will be even. Then we can apply Lemma E.3. Therefore, what we need at the moment is to keep $L \leq 2K$ after the next shot. This can be done immediately by the same manipulation explained in Lemma E.1.
Implementation
We implement the above lemmas by recursive way.
F - Strings of Eternity
Observation
Let $M = \lvert S \rvert$ and $N = \lvert T \rvert$. We replace $S$ by finitely repeated $S$ whose length is greater than $M + N$. We define $ok[i]$ for $i \in \mathbb{Z} / M \mathbb{Z}$ as follows.
$ok[i] = $ true if $T$ matches $S[i, i + N)$; false otherwise.
Then, we consider the graph whose size is $M$. We connect $i \mapsto i + N$ if $ok[i] \land ok[i + N]$ for $i \in \mathbb{Z} / M \mathbb{Z}$. This means that $T$ matches both $S[i, i + N)$ and $S[i + N, i + 2N)$, i.e., $TT$ matches $S[i, i + 2N)$. We apply this idea recursively to see that the answer is -1 if the cycle is detected. Otherwise, the answer is the maximum of the size of the connected component including $i$ where $ok[i]$ is true.
Solution
To construct $ok[i]$ in $O(N + M)$ time, we use KMP-algorithm for example.
To represent the graph and extract needed information from the graph in this problem, it is suffice to use Union-Find tree.
Tips for implement
- To repeat $S$ to the extent that its length is greater than $M + N$, we repeat constant $+ M / N$ times.
- The answer is not just the maximum of the size of the connected components. We have to check $ok[i]$.
