AtCoder Beginner Contest 134
Updated:
Source codes
Solutions
A - Dodecagon
半径 $r$ に内接する正 $12$ 角形の面積は \[ S = 12 \cdot \frac{1}{2} r^2 \sin \frac{\pi}{6} = 3r^2 \] で与えられる。これをそのまま実装すればいい。
B - Golden Apple
人が見られる木の本数は $W = 2D + 1$ 本/人なので、答えは $(N + W - 1)/W$ 人である。ここで割り算は計算機の割り算。
C - Exception Handling
解答 1
$0$-indexed とする。最大値 と 2 番目の値を求めておく。 $i = 0, 1, \dots, N - 1$ に対し、 $A[i]$ が最大値なら $2$ 番目の値を与える。
解答 2
$1$-indexed とする。便宜的に $A[0] = A[N + 1] = 0$ とする。
$X[i] = [0, i]$ における最大値、
$Y[i] = [i, N + 1]$ における最大値
と定める。これは累積 max で $O(N)$ で求まる。求めるものは $\max(X[i - 1], Y[i + 1])$ である。
ポイント
sort(B.rbegin(), B.rend()); はおしゃれでいいですね。
vector<int> B = A;
sort(B.rbegin(), B.rend());
for (auto i = 0; i < N; i++)
{
if (A[i] == B[0])
{
cout << B[1] << endl;
}
else
{
cout << B[0] << endl;
}
}
D - Preparing Boxes
解答
この問題の答えは常に Yes であり、さらに答えも $1$ 通りに決定される。 $i$ の整数が書かれた箱に入っているボールの個数を $x _ i$ とする。
その方法。 $i = N , N - 1, \dots, 1$ に対して、順番に条件を充たすようにボールを入れていくことを考える。今簡単のため $N \approx 10^5$ とする。すると最初は $x _ N = a _ N$ 個入れるしかない。次も $x _ {N - 1} = a _ {N - 1}$ 個入れるしかない。これを繰り返していくと $i = N / 2$ の時に、 $x _ {N} + x _ {N / 2} = a _ {N / 2}$ が要求されるが、ここで $x _ N$ はすでに決まっているから $x _ {N / 2}$ も決定される。もっと一般にいうと、上から $a _ i$ の条件を吟味していくと \[ \sum _ {j = i, 2i, \dots ki \leq N} x _ j = a _ i \] となるので、 \[ x _ i = a _ i - (x _ {2i} + x _ {3i} + \dots + x _ {ki}) \tag{D.1} \] となる。ただしここで演算は $\mathbb{Z}/2\mathbb{Z}$ である。これで答えが求まる。
ポイント
(D.1) 式の和をとる際に j += i と書くところをミスって 1WA した。
E - Sequence Decomposing
解答
基本的には $i$ を前から見ていき、「同じ色で塗った数のうち、一番大きな数」を貪欲法でシミュレーションをして保持していけばよろしい。今まである色のうち、それより小さい数字で、かつ、一番大きい数字の色で塗るのが最善である。ただしデータ構造を工夫して $O(\log N)$ でやる必要がある。
どういうことかというと、まず $S = \emptyset$ とする。 $S$ に二分探索系の STL アルゴリズムを適用したい。そのためのコンテナの条件は、以下の通り。
- 昇順または降順に常に並んでいる (前提条件)
- ランダムアクセスをサポートしている (concept) … これは $O(\log N)$ でやるため。
- 先頭か末尾の挿入が $O(1)$ である (concept)
Review 時の方針
まず $A[i]$ たちに $-1$ をかけて、大小関係を逆転する。「それより大きい数字で、かつ、一番小さい数字」を取り出すようにする。するとこれは upper_bound でできる。発見できなかった場合、挿入は末尾になる。発見できた場合は、その数字を書き換える。よって vector で可能である。
for (auto i = 0; i < N; ++i)
{
auto it{upper_bound(V.begin(), V.end(), A[i])};
if (it == V.end())
{
V.push_back(A[i]);
}
else
{
*it = A[i];
}
}
答えは V.size() である。
解説放送の方針
int p = lower_bound(S.begin(), S.end(), A[i]) - S.begin(); とする。 $p = 0$ であれば、 $S$ の冒頭に $A _ i$ を入れるしかない。つまり違う色で塗るしかない。そうでなければ $S[p - 1]$ の色で塗るのがベストである。 $S[p - 1] \gets A _ i$ と書き換える。いずれの操作でも昇順であるという前提条件は保証されている。
上の 2 つの条件を充たすデータ構造として deque<int> D; を用いればよろしい。また、逆順に持っておけば末尾に挿入することに相当するので vector<int> V; について auto it = lower_bound(V.rbegin(), V.rend(), A[i]); としても良い。
ランダムアクセスはサポートされていなくてもいい(例えば set<int> S;)が、これは値の書き換えができない分、難しくなる。
別解
Dilworth の定理というのがあるらしい。
DAG について、 最小パス被覆の本数は、任意の 2 点間にパスが存在しないような頂点の最大部分集合の元の個数に等しい
今回の場合、頂点集合 $\{ (i, A _ i) \}$ に対して、 $e = ((i, A _ i,), (j, A _ j))$ に辺があるとは、 $i < j$ かつ $A _ i < A _ j$ であることとする。するとこのグラフは DAG である。そして答えは最小パス被覆の個数に等しい。その順番に同じ色で塗っていけばいいからである。
そこで「任意の 2 点間にパスが存在しないような頂点の最大部分集合」を求めれば答えに至るわけだが、この集合は $A _ i$ について見ると、最大の広義単調減少列を求めていることに等しい。
ポイント
前提条件と concept をはっきりさせるのが大事だと思った。
F - Permutation Oddness
着想
これは箱根駅伝 DP と呼ばれるものを使う。
$0$-indexed とする。まず答えの言い換えをする。 $p \in \mathfrak{S} _ N$ とする。 $p$ の奇妙さを $f(p)$ と書く。 $p \colon N \to N$ である。これを辺の結び方と見る。つまり、左と右に集合 $N = \{ 0, 1, \dots, N - 1 \}$ を縦に並べてかき、そこに $(i, p _ i)$ に辺を張ることにする。 $i - 1, i$ の間に点線 $l _ i$ を書き、それと辺との交点の数を $a _ i$ とする。すると \[ f(p) = \sum _ {i = 1}^{N - 1} a _ i \tag{F.1} \] が成立する。図の例を参照。
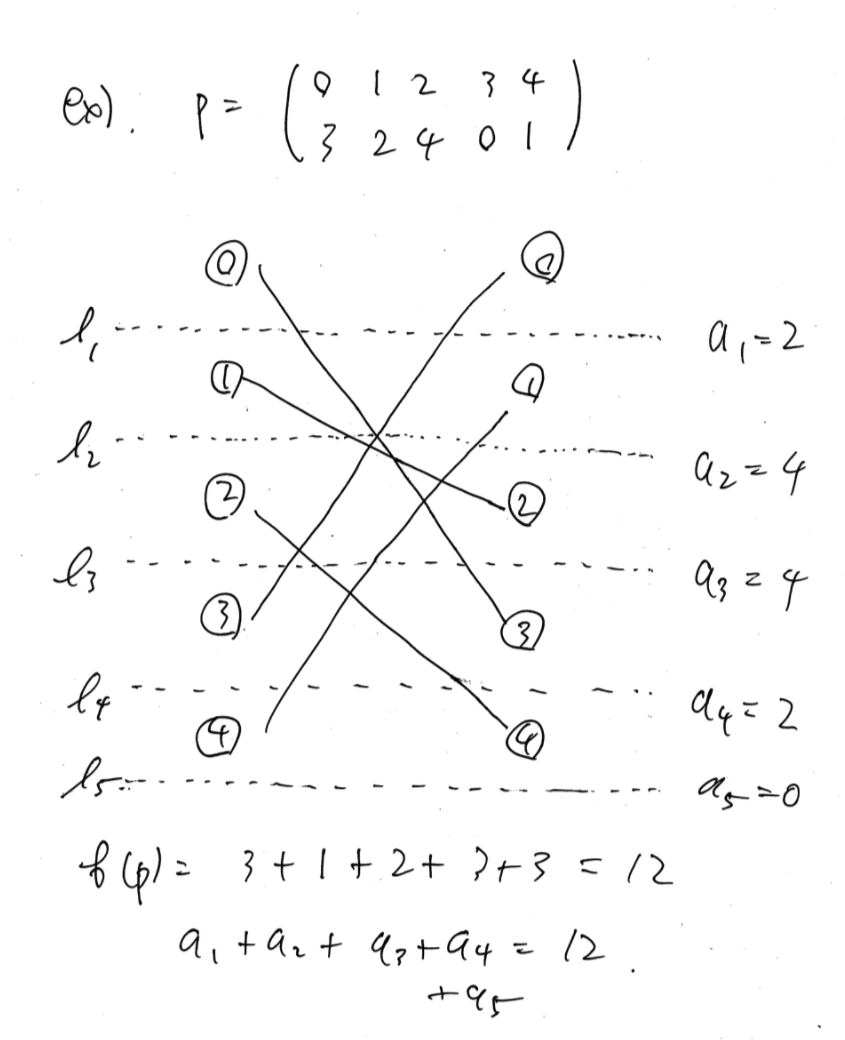
これはなぜかというと、ある辺 $(k, p _ k)$ と $\{ l _ i \} _ i$ たちの交点の数は $\lvert i - p _ i \rvert$ 個に等しいからである。これを $l _ i$ ごとに数え上げたのが (F.1) の右辺である。こういう理屈である。
また、奇妙さが奇数であることはありえないので、 $K$ が奇数のときは即座に $0$ を出力する。以下奇妙さは $2$ で割った値を採用するものとする。
DP part
Definition
$DP[i][j][k] = $「 $\sum _ {x = 1} ^ i a _ x = k$ を充たす場合の数。ただし、 $0$ から $i - 1$ までの頂点のうち $j$ 個を保留にしている(両側同じ数なので、それを $j$ とおいている)。
「保留」とは、その頂点を後で $i + 1$ より大きい頂点と結ぶことをいう。つまり保留になっている頂点の数が $l _ i$ との辺の交点の個数に一致する。
DP の遷移
Initial state
$DP[0][0][0] = 1$, otherwise $0$.
Answer
$DP[N][0][K]$.
Transition
配る DP でいける。 $i = 0, \dots, N - 1$, $j = 0, \dots, i$, $k = 0, \dots, K$ に対して、 $DP[i][j][k]$ の遷移の仕方は次の $4$ パターンがある。
- 左右の $i$ を結ぶ場合:この場合 $j$ は変化しないので、 $l _ i$ とは $j$ 個交わる(奇妙さを $2$ で割っていることに注意)。つまり、次の通り。 \[ DP[i + 1][j][k + j] \mathbin{ {+} {=} } DP[i][j][k]. \]
- 左右の $i$ を保留する場合:この場合 $j$ は $1$ 増える。 $l _ i$ とは $j + 1$ 個数交わる。つまり、次の通り。 \[ DP[i + 1][j + 1][k + j + 1] \mathbin{ {+} {=} } DP[i][j][k]. \]
- 左右の $i$ の片方を保留し、片方を過去保留してあったものと結ぶ場合:この場合 $j$ は変化しない。結ぶ方の結び方は $2j$ パターンある。つまり、次の通り。 \[ DP[i + 1][j][k + j] \mathbin{ {+} {=} } DP[i][j][k] \times 2j. \]
- どちらも片方を過去保留してあったものと結ぶ場合:この場合 $j$ は $1$ 減る。つまり $j \geq 1$ が必要である。結ぶ方の結び方は $j^2$ パターンある。つまり、次の通り。 \[ DP[i + 1][j - 1][k + j - 1] \mathbin{ {+} {=} } DP[i][j][k] \times j^2. \]
ポイント
これは知らなかった。昔からの定跡らしいが初めて見た。
Others
踏んだり蹴ったりの成績でした。ひどいひどい。
