AtCoder Grand Contest 035
Updated:
Source codes
Solutions
A - XOR Circle
解答
最初に $x$ をおき、次に $y$ をおくと、その次は $x \oplus y$ に決まる。その次は $y \oplus (x \oplus y) = x$ になり、その次は $y$ になる。つまり周期 $3$ である。
$N$ が $3$ の倍数でないとき
$x = y = x \oplus y$ が必要である。つまり $x = y = 0$ が条件である。すべての数字が $0$ の場合のみ Yes である。
$N$ が $3$ の倍数のとき
出てくる数字の種類で場合分けをする。
- $4$ 種類以上:
Noである。 - $1$ 種類:上に帰着する。
- $2$ 種類:$x, 0, x$ を繰り返すしかない。つまり $0$ が $N/3$ 個、それ以外の数 $x$ が $2N/3$ 個が条件。
- $3$ 種類: $x, y, z$ とあったとき $x \oplus y \oplus z = 0$ かつそれぞれ $N/3$ 個が条件である。
ポイント
この通りに実装してこの通りに AC できた。
B - Even Degrees
判定部分
$M$ が奇数のとき、答えは No である。
逆に $M$ が偶数の時は必ずできる:適当に向きを定めたとする。ある頂点 $v$ が存在して、出次数が奇数であるとする(ないならその時点でできたことになる)。このとき、 $v \neq w$ をみたす頂点 $w$ が存在し、出次数が奇数である。存在しなければ $M$ が偶数であるという条件に反するからである。グラフは連結であるので、 $v, w$ を結ぶ path が存在する。その path の方向を全部逆にすると、 $v, w$ 以外の出次数の偶奇はそのままで、 $v, w$ だけが変わる。つまり奇数になる。これを繰り返せば答えは Yes である。
構築部分
次の定理は容易に示される。
定理:グラフ $M$ は $0$ を根とする木であるとする。各頂点ごとに、出次数が偶数であるべきか奇数であるべきかが決まっていると仮定する。この時、 $0$ 以外の頂点では、その条件をすべて充たすように辺に向きをつけることが可能である。
証明:葉から順番に向きを決定していけばよろしい。というか向き付けの方向は $1$ 通りしかない。
さて問題に戻る。可能判定をする。可能である場合が問題である。まずグラフ $M$ に対して適当な全域木 $T$ をとる。 $M \setminus T$ の各辺に対して好きなように向きを定める。すると各頂点で $T$ において出次数が偶数であるべきか奇数であるべきかが定まっているので、定理が適用できる。問題は根の部分だが、これは可能判定の時点で自動的に条件が充たされている。
ポイント
グラフ $M$ に対して全域木 $T$ を構築するのがポイント。偶数にこだわりすぎて構築できなかった。
C - Skolem XOR Tree
解答
まず $N = 1, 2$ の場合は No である。
次に $N$ が $2$ 冪の場合も No である。 $N$ と $N + N$ の間で $N$ の bit を立たせることができないからである。
その他の場合は実は全てできる。まず $N = 3$ の木を作る: $(1, 2)$, $(2, 3 + N)$, $(1, 3)$, $(3, 2 + N)$, $(2 + N, 1 + N)$.
$N$ が奇数の場合は以下のようにして $1$ の周りに繋げることでできる: $(1, i)$, $(1, i + 1)$, $(i + 1, i + N)$, $(i, i + 1 + N)$. これを繰り返す。
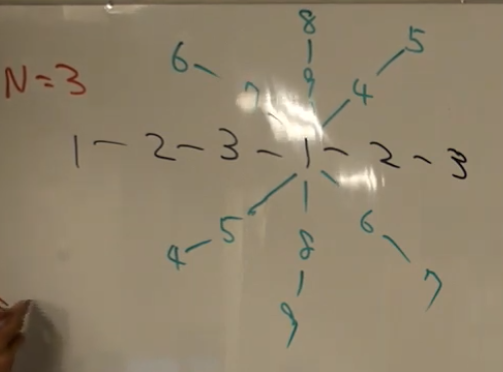
問題は $N$ が偶数の場合である。この時はある $a, b$ を発見して $(N, a)$, $(a, 1)$, $(1, b)$, $(b, N + N)$ というようにしたい。これはつまり $N \oplus 1 = a \oplus b$ である。 $a, b$ は違う bit を立たせるようにする。 $N \oplus 1 = N + 1$ であるから、 $a$ は $N$ の最高 bit として、 $b = N + 1 - a$ とするとうまくいく。
ポイント
構築は時間内では無理です。すみません。
D - Add and Remove
考察
$0$-indexed とする。最終結果は必ず以下の形をしている。 \[ \sum _ {i = 0} ^ {N - 1} w _ i A _ i. \] この $\{ w _ i \}$ の組を全て試せば答えが出る。しかしそれではもちろん間に合わないので何らかの高速化をする必要がある。ひとまず $\{ w _ i \}$ の生成方法を考察する。
長さ $k$ の列 $\{ w _ i \}$ の生成方法を全てわかっているものとする。このとき長さ $k + 1$ の列 $\{ w _ i ‘ \}$ を生成する方法を全て出力する方法を考察する。まず最初に $i$ を食べたとすると、カードの列は \[ A _ 0, A _ 1, \dots, A _ {i - 1} + A _ i, A _ i + A _ {i + 1}, \dots, A _ {k + 1} \] となる。これは長さ $k$ であるから、答えは \[ w _ 0 A _ 0 + w _ 1 A _ 1 + \dots + w _ {i - 1} (A _ {i - 1} + A _ i) + w _ i (A _ i + A _{i + 1}) + \dots + w _ k A _ {k + 1} \] つまり $\{ w _ i ‘ \}$ は次の通りである。 \[ w _ 0, w _ 1, \dots, w _ {i - 1}, w _ {i - 1} + w _ i, w _ i, \dots, w _ k \] これはつまりどういうことかというと、
- 最初は $1, 1$ から出発する。
- 中に好きな場所を選んで、そこにその隣の数の和を入れていく。
これで $\{ w _ i \}$ を全て求めることができる。
DP に変換する
最終的に和の最小値をとるので、区間について、真ん中の数字は忘れて最小値だけ保持しておけばよろしい。関係があるのは区間の端の数字だけである。そこでメモ化再帰をする。
$calc(l, r, x, y) = $ 区間 $[l, r)$ の最小値。ただし $w _ l = x$ であり $w _ r = y$ であるものとする。
答えを出す際にはメモ化で十分である。 $x$ と $y$ の種類はカタラン数程度しかないので map<ll, map<ll, ll>> memo[20][20]; で実は保持できる。
答え: $calc(0, N, 1, 0)$ 。計算: まず $l + 1 = r$ の場合、 $calc(l, r, x, y) = x A _ l$ である。次に「最初は $1, 1$ から出発する」を処理する必要がある。つまり $calc(0, N, 1, 0) = calc(0, N - 1, 1, 1) + A _ {N - 1}$ である。その他は以下の通りに計算される。 \[ calc(l, r, x, y) = \min _ {l < i < r} \left( calc(l, i, x, x + y) + calc(i, r, x + y, y) \right). \]
ポイント
これはなかなか難しい。特に $x, y$ はカタラン数程度しかないというのは一生気づかないと思う。
E - Develop
放棄。これはわからなくて良さそう。
F - Two Histograms
考察
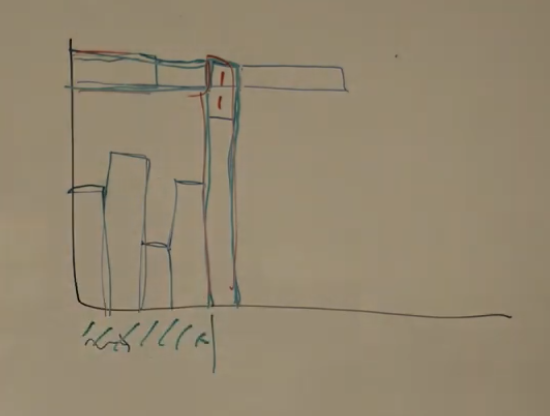
まずある行と列のヒストグラムが以下のようになっているものとする。

この 2 つは同じ盤面の結果を与える。だからどちらか一方だけを数え上げる必要がある。
定理:図の右側のパターンを禁止し、全て左側に置換したと仮定する。このとき、結果の盤面を与えるヒストグラムは一意に定まる。
証明:あるヒストグラム $A, A’$ が存在し、両方とも同じ盤面を与えたとする。背理法で示す。結論を否定し、ある列 $i$ があって、 $A$ と $A’$ では $j < i$ までは同じ高さを与えており、第 $i$ 列では違う高さを与えていると仮定する。 $A’$ の方が高いと仮定して一般性を失わない。このとき、 $A’$ の第 $i$ 列で一番高い高さの行を考察する。このマス目の数字は $1$ でなければならない。 $0$ であれば $A’$ のヒストグラムに矛盾するし、 $2$ であれば $A$ のヒストグラムに矛盾するからである。 $A’$ のヒストグラムは、このマスを列の高さで覆っているが、 $A$ のヒストグラムは、このマスを行の横幅で覆っていることになる。つまり $A$ のこの行のヒストグラムは、この列までは確実に覆っている。さらに「$j < i$ までは同じ高さを与えている」の仮定から、 $A$, $A’$ ではこの列までは全く同じ必要がある。つまり $A’$ においても、$j < i$ までは覆っていることになる。しかし $j = i$ のところは、先ほどの議論により覆っていない。よって $A’$ のこの行のヒストグラムの長さは $i - 1$ で確定する。これは禁止パターンができたことになる。これは矛盾である。よって列について $A$ と $A$ のヒストグラムが一致する。よって行についても一致する他なく、 $A = A’$ が従う。
包除原理による解答
したがって、禁止パターンのヒストグラムがどれだけ含まれているかで包除原理に帰着されて答えが求まる。必要なら swap することにより $N \leq M$ を仮定して一般性を失わない。
$X[i] = $ 禁止パターンを形成する行列が少なくとも $i$ 個含まれているヒストグラムの定め方の場合の数
とすると、答えは次式で与えられる。 \[ ans = \sum _ {i = 0} ^ N (-1) ^ i X[i]. \tag{F.1} \]
$X[i]$ は直接記述できる。まず禁止パターンの行・列の選び方は \[ \begin{pmatrix} N \\\ i \end{pmatrix} \begin{pmatrix} M \\\ i \end{pmatrix} \] 通りある。これの「組み合わせ」に $i!$ 通りある。残りの部分は自由に高さを決めていいので $(M + 1)^{N - i} (N + 1)^{M - i}$ 通りある。つまり、 \[ X[i] = \begin{pmatrix} N \\\ i \end{pmatrix} \begin{pmatrix} M \\\ i \end{pmatrix} i! (M + 1)^{N - i} (N + 1)^{M - i} \tag{F.2} \] である。(F.1) と (F.2) で $ans$ は求まる。
ポイント
解くのは無理だろうが、理解はできる。
