AtCoder Grand Contest 032
Updated:
Source codes
Solutions
A - Limited Insertion
解答
クエリを逆順に処理することを考える。すると挿入した座標 $=$ その数字なので、直前に挿入する数字が何であったのかの候補が決まる。そのうち一番大きいものを挿入するのが正解である。仮に $i < j$ が挿入可能であるならば $j$ の方を挿入していないとおかしい。というもの $i$ を挿入していたとすると $j$ 番目の方は $j - 1$ 以下の座標になるので、どうやっても挿入できない。以上により挿入の仕方は事実上 $1$ 通りに決定される。途中で挿入できなければ負けで、そうでなければ勝ち。
ポイント
A にしては難しいとのことであった。
B - Balanced Neighbors
解答
まず完全グラフを考える。すると全体の合計に自分自身を除いた数になる。これから削る方針でする。
$N$ が奇数の場合
($i$ と $N - i$) たちを削ったものが正解。
$N$ が偶数の場合
($i$ と $N + 1 - i$) たちを削ったものが正解。
ポイント
気づけばすぐ。
C - Three Circuits
解答
まず全部の頂点の次数が偶数でないとアウトである。この時点でオイラーグラフであることは確定である。一本道がある。
次数 $6$ 以上の頂点が存在する場合は、答えは “Yes” である。その点でオイラー路を分割すればサーキットが 3 つ得られる。以下そうでない場合を考える。
次数 $4$ の頂点が存在しない場合は、交わりのない閉路であるから、分割しようがない。これは “No” である。次数 $4$ の頂点が $1$ 個の場合も、サーキットは $2$ つまでしかできない。次数 $4$ の頂点が $3$ 個の場合は必ずできる(解説放送下図の場合分け参照)。次数 $4$ の頂点が $2$ 個の場合は場合分けが必要である。その頂点を $s, t$ とし、 $s \to t$ へ DFS をする。この時 $s$ から $t$ にたどり着かずに $s$ に戻って来る場合は答えは “No” である。
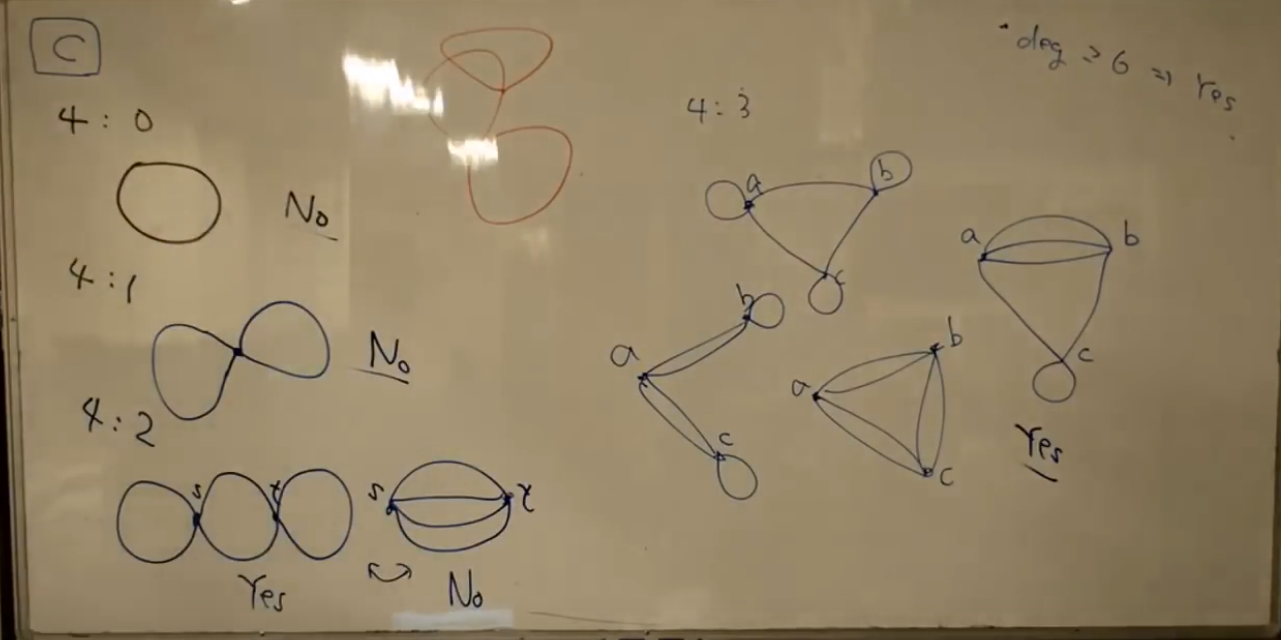
ポイント
実験、考察、一般論を導くしかないだろう。
D - Rotation Sort
問題文の言い換え
$1$-indexed とする。まず問題文の状況と $2$ つの操作を言い換える。次の問題と同値である。
$p _ 1, p _ 2, \dots, p _ N$ が数直線上にこの順序で並んでいる。ただしその絶対的な位置は問わないとする。以下の操作が好きな順序で何度でも可能である。
- コスト $A$ を支払う。好きな数字を数直線上から取り出し、その座標を大きくして、配置し直す。
- コスト $B$ を支払う。好きな数字を数直線上から取り出し、その座標を小さくして、配置し直す。
相対的な数字の順序が $1, 2, \dots, N$ になるまでの最小コストを求めよ。
これを DP で解くために、最初の数直線の状態 $X$ と、最後の数直線の状態 $Y$ を縦に並べる。そしてこれに布を被せて、左から順番に reveal していくと考える。すると以下のことが言える。まず reveal すると $X$ は $p _ 1, p _ 2, \dots, p _ N$ の順番で数字が登場するし、 $Y$ は $1, 2, \dots, N$ の順番で登場する。上に新しく $p _ i$ が登場するとき、コストの計算をすることを考える。まず $p _ i$ が $Y$ ですでに登場していた場合は、それは座標を小さくして配置し直したということだから、コスト $B$ が支払われる。同様に、 $Y$ に登場していなかった場合は、コスト $A$ が支払われる。同時に登場していた場合は、コスト $0$ が支払われて、先に進む。
DP で問題を解く
$DP[i][j] = X$ 上で $p _ i$ まで reveal されていて、 $Y$ 上で $j$ まで reveal されている段階で支払われている最小コスト
と定義する。初期状態: $DP[0][0] = 0$, otherwise $DP[i][j] = \infty$. 答え: $DP[N][N]$. 遷移: $i = 0, \dots, N$ に対し、 $j = 0, \dots, N$ に対し、
\[
\begin{align}
DP[i][j + 1] &\gets \min(DP[i][j + 1], DP[i][j]) & & j < N, \\
DP[i + 1][j] &\gets
\begin{cases}
\min(DP[i + 1][j], DP[i][j] + B) & p _ {i + 1} \leq j, \\
\min(DP[i + 1][j], DP[i][j] + A) & p _ {i + 1} > j,
\end{cases} & & i < N, \\
DP[i + 1][j + 1] &\gets \min(DP[i + 1][j + 1], DP[i][j]) & & i < N \land j < N \land p _ {i + 1} = j + 1.
\end{align}
\]
ポイント
ローテーションの言い換えは思いつかなかった。記憶しておきたい。
E - Modulo Pairing
問題の解析
$a _ i$ たちは昇順で sort されているとして良い。 $a, b < M$ および $\mathbb{Z}/M\mathbb{Z}$ 上で加法を考察しているから、ペアの作り方によりコストは結局、
\[
\mathop{cost}(a, b) =
\begin{cases}
a + b & a + b < M, \\
a + b - M & a + b \geq M
\end{cases}
\]
であることに注意されたい。上の場合を青のペア、下の場合を赤のペアと呼ぶことにする。
まず補題を示す。
補題: $(a, b)$ が赤のペアであり、かつ、 $(c, d)$ が青のペアであると仮定する。このとき、 $a, b \geq c, d$ を仮定しても、最小値が達成される。
証明:最小値が達成され、かつ、 $a < c$ であると仮定する。このとき、 $a + d < c + d < M$ が成立する。よって $\mathop{cost}(a, d) < \mathop{cost}(c, d)$ である。また、 $b + c > a + b \geq M$ より、 $\mathop{cost}(b, c) = b + c - M$ である。そして $b - M < 0 \leq d$ より、次式が成立する。 \[ \mathop{cost}(b, c) = b + c - M < c + d = \mathop{cost}(c, d). \] 以上より、 $\mathop{cost}(a, d), \mathop{cost}(b, c) < \mathop{cost}(c, d)$ であるから、 $a, c$ を swap しても最小値を達成することがわかる。これが示すことであった。
実装
補題より、ある $0 \leq t \leq N$ が存在し、 $0 \leq i < 2t$ に関しては青のペア、 $2t \leq i < 2N$ に関しては赤のペアを作るとして最小値を探索すればよろしい。それぞれの区間では最大値の最小値を達成するためには、大きいものと小さいものを順に組み合わせれば良いのはさすがに自明であろう。そしてそれに気づけば、 $t$ が小さければ小さいほど、最大値が小さくなるのも明らかであろう。ただし「赤のペア」は、前提として和が $M$ 以上である必要がある。だから $t$ が小さすぎると正しい分け方ができない。よってめぐる式二分探索で書けばよろしい。 $ok = N + 1$, $ng = -1$ としてやればよろしい。
ポイント
実装は信じられないくらい簡単なのだが、着想が難しい。しかし 1200 点だから絶対手が出ないレベルではない。
F - One Third
Analyse the manipulation
We make points on the circle $[0, 1]$. Red points are cut points. Blue points are $+ 1/3$ points of reds. Green points are $- 1/3$ points of reds. Then, the segments $[0, 1/3)$, $[1/3, 2/3)$ and $[2/3, 1)$ have the same shape. Let $I = [0, 1/3)$ and fix one red point as $0$. Then, $(0, 1/3)$ has $N - 1$ points.
The original manipulation is equivalent to the following manipulation.
We put $N - 1$ points on $I$ uniformly randomly. After that, we color each of them as red, blue, or green, randomly. Here, $0$ is red and $1/3$ is blue.
We assume $1$-indexed and we promise that $0$ is the $0$-th point and $1/3$ is the $N$-th point.
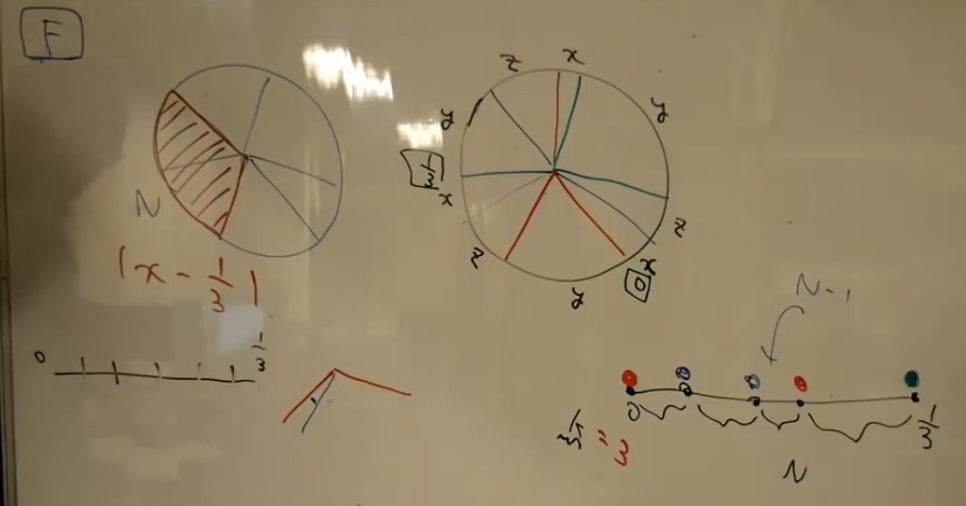
Then, $\lvert x - 1/3 \rvert$ is the minimum value of the length of the segments whose edge points are differently colored. We say that a segment is differently colored if its edge points are different colored. We focus on how many segments are differently colored. We use $k$ to denote this value. The answer is the following. \[ E = \sum _ {k = 0} ^ N \frac{C _ k}{3 ^ {N - 1}} E _ k. \]
Here we have used $C _ k$ and $E _ k$ as follows.
$C _ k = $ the number of possibility to color out $N - 1$ points,
$E _ k = $ the estimate value of the minimum value of the length of the differently colored segments.
Calculation of $C _ k$
Fix $k$ as defined above. $I$ has $k$ differently colored segments and $N - k$ are same-colored.
First, we exclude same-colored segments. Th number of choices is $\begin{pmatrix} N \ k \end{pmatrix}$. Note that the number of the points are $N - 1$, and this means that we can ignore $N - k - 1$ points, or we can assume that they are pressed. Thus hereinafter we think of $k$ points.
Second, we think of the color of these $k$ points. We generate $k$ differently colored segments. The number of possibility is calculated by typical DP.
Definition
$dp[i][j] = $ the number of the possibilities: We have determined $[0, i]$-th elements. Each segments are differently colored. The color of the last segment is $j$, where $j = 0$ means red, $j = 1$ blue and $j = 2$ green.
Initial state
$dp[0][0] = 1$, otherwise $0$.
Answer
\[ C _ k = \begin{pmatrix} N \\ N - k \end{pmatrix} dp[k][1]. \]
Transition
For $i = 1, \dots, N$, for $j = 0, 1, 2$, we execute the following. \[ dp[i][j] \gets dp[i - 1][(j + 1) \% 3] + dp[i - 1][(j + 2) \% 3]. \]
Calculation of $E _ k$
We see that \[ E _ k = \frac{1}{3} \cdot \frac{k}{N} \cdot L _ k, \] where
$L _ k = $ the expected value of the minimum of the length of the segment on $[0, 1)$ where we put $k - 1$ points uniformly randomly.
We compute $L _ k$ by integral. But before that, we show an important formula about expectation in discrete case.
\[
\begin{align}
\sum _ {k = 0} ^ N X P (X = k)
&= 0 P(X = 0) + 1 P(X = 1) + \dots + N P(X = N) \\
&= P(X \geq 1) + \dots + P(X \geq N) \\
&= \sum _ {k = 1} ^ N P(X \geq k). \tag{F.1}
\end{align}
\]
Going back to the original problem, we use $X$ to denote the minimum of the length. Fix $0 \leq x \leq 1 / k$. We compute the probability of the event $X \geq x$. First we spare $x$ for each segments. Then, we see that the probability is equal to the probability that we put all the points into the remaining, i.e., $(1 - kx) ^ {k - 1}$.
Then, we apply (F.1) to this continuous case. That is, we calculate the integral.
\[
\begin{align}
L _ k &= \int _ 0 ^ {1 / k} (1 - kx) ^ {k - 1} dx \\
&= \left[ - \frac{1}{k ^ 2} (1 - kx) ^ k \right] _ 0 ^ {1/k} = \frac{1}{k ^ 2}.
\end{align}
\]
Therefore, we conclude that
\[
E _ k = \frac{1}{3 N k}.
\]
