AtCoder Grand Contest 031
Updated:
Source codes
Solutions
A - Colorful Subsequence
'A' から数え始めて $i$ 番目の文字の個数を $cnt[i]$ とする。この中から $0$ 個以上 $1$ 個以下をそれぞれ取ればいいので、答えは以下で与えられる。 $-1$ は空文字の分である。
\[ \left( \prod _ {i = 0} ^{25} cnt[i] \right) - 1. \]
B - Reversi
$0$-indexed とする。
解答の方針
例があったほうが簡単なので \[ 1, 3, 1, 2, 3, 3, 2 \] を使う。これの最終形として \[ (1, 1, 1), (2, 2, 2, 2) \] が考えられる。それぞれのグループ(数は異なるものとする)の右端と左端を考えると、必ず元の数列と一致していなくてはならない。というのも $x \dots [x] y \dots y$ の $[x]$ が $z \mapsto x$ と変換されたとすると、その前状態からどこかで挟まれていないとおかしいので $xxx$ となるが、 $[x] y$ の $y$ の部分は $[x]$ と同じ色で永遠に塗られることになって不合理である。ゆえに元の数字と一致している必要がある。逆に元の数字と一致していれば実際にそれを作るのは簡単である。ただ右端と左端を選べばいいからである。
そこで上の $(1, 1, 1)$ と $(2, 2, 2, 2)$ の間に元の数列で仕切りを入れることを考察する。つまり $1, 3, 1, / 2, 3, 3, 2$ のようにする。
DP で解答を出す
まず $C _ {N} = -1$ と番兵をいれておく。
$DP[i] = i - 1$ 番目と $i$ 番目で仕切りの必ずいれるとして、 $C _ 0, \dots, C _ i$ までに作られる盤面の個数
と定めると、初期状態: $DP[0] = 1$, 答え: $DP[N]$, 遷移: $i = 1, \dots, N$ に対し、 $C _ {i - 1} = C _ {i}$ ならば $DP[i] = DP[i - 1]$, そうでないならば、 \[ DP[i] = DP[i - 1] + \sum _ {j < i - 1, C _ j = C _ {i - 1} } DP[j]. \tag{B.1} \] これは正しい遷移であるが $O(N^2)$ になる。和のところを別途持っておけば計算量が落とせる。
$sum[c] =$ それまで見てきた $j$ に対し $\sum _ {C _ j = c} DP[j]$.
を持っておけば、 (B.1) の遷移は以下のようになる。
\[
\begin{align}
DP[i] &= DP[i - 1] + sum[C _ {i - 1}], \\
sum[C _ {i - 1}] & \mathbin{ {+} {=} } DP[i - 1].
\end{align}
\]
計算量は $O(N)$ である。
少しわかりにくかったら、同じ色が連続する区間は $1$ 個の石であるとして良い。
C - Differ by 1 Bit
解答
この問題は、以下の問題に言い換えられる。
$2^N = \{ 0, \dots, 2^N - 1 \}$ を頂点とし、 $1$ bit だけ異なるところに辺を張ったグラフで $A$ から $B$ への一筆書き路(ハミルトンパス)を構成せよ。可能であるなら構成し、可能でないなら
"NO"と出力せよ。
まずこのグラフ $G$ は連結な二部グラフである。全ての頂点を経由するので、 $A, B$ では色が違っていないといけない。色が同じなら答えは "NO" である。
逆に色が違っていれば、答えは "YES" である。以下これを $N \geq 1$ についての数学的帰納法で示す。 $N = 1$ のとき、 $0$ と $1$ を繋げるだけなので可能である。 $N$ で可能であるとして $N + 1$ で可能であることを示す。まず $A$ と $B$ で bit が違う桁があるはずなので、これを $i$ とする。この時、部分グラフ $G _ A, G _ B$ の頂点を
$G _ A = \{ X \in 2^{N + 1} \mid X[i] = A[i] \}$,
$G _ B = \{ X \in 2^{N + 1} \mid X[i] = B[i] \}$
と分ける。辺も分ける。仮に $\sharp G _ A = 1$ の場合は、問題全体が $N = 1$ に帰着されるので可能である。 $N \geq 1$ の場合は、 $G _ A$ の中で $A$ と異なる色で塗られている頂点がある。これを $C$ とする。また、 $C$ と $i$ 桁目が異なる頂点 $D$ が $G _ B$ に存在するが、これは $G$ 上で $C$ と辺を共有しており、 $B$ と色が異なる。帰納法の仮定により $G _ A$ 上で $A \to C$ のハミルトンパスが存在する。そして $C \to D$ はただ辺を移動するだけである。そして $G _ B$ 上で $D \to B$ のハミルトンパスが存在する。これらをくっつけることにより、 $G$ 上での $A$ から $B$ へのハミルトンパスが得られる。
解説放送の図がわかりやすいので貼り付けておく。 $N = 3$ の場合。
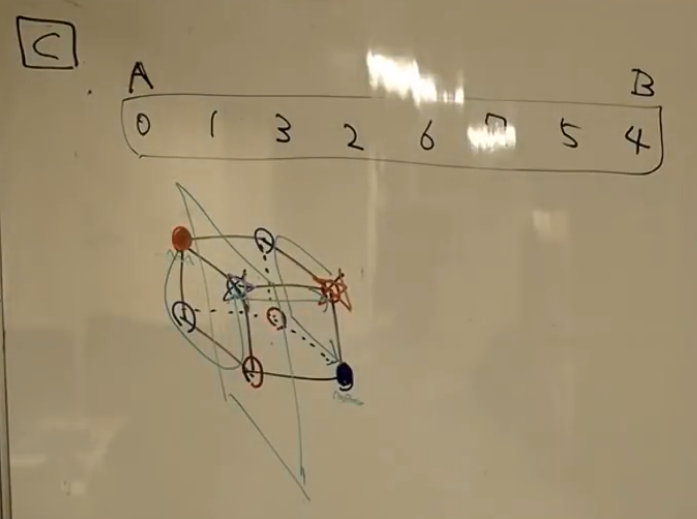
実装
数学的帰納法で示したことを普通に実装するためには再帰を使うのが一番いいだろう。部分グラフは $mask$ で bit を立たせて管理すればよろしい。 $mask$ の立っている bit が $N - 1$ 個の時は順番に挿入して終わり。そうでない時は新しい部分グラフを作るために $new_mask$ を生成する。続けて $A$ から $new_mask$ 上で $1$ つずれたものを $C$ として、そこから $D$ を生成する。後は dfs(A, C, new_mask);, dfs(D, B, new_mask); とする。もちろん初期状態は dfs(A, B, 0); である。
void dfs(int A, int B, int mask)
{
if (cnt(mask) == N - 1)
{
ans.push_back(A);
ans.push_back(B);
return;
}
int ind;
for (ind = 0; ind < N; ind++)
{
if (mask >> ind & 1)
{
continue;
}
if ((A >> ind & 1) != (B >> ind & 1))
{
break;
}
}
int new_mask = mask | 1 << ind;
int next;
for (next = 0; next < N; next++)
{
if (new_mask >> next & 1)
{
continue;
}
break;
}
int C = A ^ 1 << next;
int D = C ^ 1 << ind;
dfs(A, C, new_mask);
dfs(D, B, new_mask);
}
ポイント
まず二部グラフでハミルトンパスを検討する問題だということに気がつく必要がある。 $N = 3$ で方針が立った後は、以降は一直線だと思う。
D - A Sequence of Permutations
解答
$0$-indexed とする。 $f \colon \mathfrak{S} _ N \times \mathfrak{S} _ N \to \mathfrak{S} _ N$ を $f(p, q) = q p ^ {-1}$ と定めている。
性質があると信じて実験をする。 $a, b \in \mathfrak{S} _ N$, $A = a^{-1}$, $B = b^{-1}$ とする。
\[
\begin{align}
X _ 0 &= a, \\
X _ 1 &= b, \\
X _ 2 &= bA, \\
X _ 3 &= bAB, \\
X _ 4 &= bABaB, \\
X _ 5 &= bABaBbaB = bABaaB, \\
X _ 6 &= bABaaBbAbaB = bABabaB, \\
X _ 7 &= bABabaBbAAbaB = bABabAbaB, \\
X _ 8 &= bABabAbaBbABAbaB = bABabAAbaB, \\
X _ 9 &= bABabAAbaBbABaBAbaB = bABabABAbaB, \\
X _ {10} &= \dots
\end{align}
\]
これだけだとわからんだろうから、プログラムを書いて実験し、後ろの方を眺める。
\[
\begin{align}
X _ {50} &= bABabABabABabABabABabABabABabABabAAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {51} &= bABabABabABabABabABabABabABabABabABAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {52} &= bABabABabABabABabABabABabABabABabABaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {53} &= bABabABabABabABabABabABabABabABabABaaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {54} &= bABabABabABabABabABabABabABabABabABabaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {55} &= bABabABabABabABabABabABabABabABabABabAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {56} &= bABabABabABabABabABabABabABabABabABabAAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {57} &= bABabABabABabABabABabABabABabABabABabABAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {58} &= bABabABabABabABabABabABabABabABabABabABaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {59} &= bABabABabABabABabABabABabABabABabABabABaaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {60} &= bABabABabABabABabABabABabABabABabABabABabaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {61} &= bABabABabABabABabABabABabABabABabABabABabAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {62} &= bABabABabABabABabABabABabABabABabABabABabAAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {63} &= bABabABabABabABabABabABabABabABabABabABabABAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {64} &= bABabABabABabABabABabABabABabABabABabABabABaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {65} &= bABabABabABabABabABabABabABabABabABabABabABaaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {66} &= bABabABabABabABabABabABabABabABabABabABabABabaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {67} &= bABabABabABabABabABabABabABabABabABabABabABabAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {68} &= bABabABabABabABabABabABabABabABabABabABabABabAAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaBAbaB, \\
X _ {69} &= \dots.
\end{align}
\]
すると自然に $x = bABa$, $y = AbaB$ と縮約してみようかなと思い始める。すると以下のようになる。
\[
\begin{align}
X _ {50} &= xxxxxxxxbAyyyyyyyy, \\
X _ {51} &= xxxxxxxxbAByyyyyyyy, \\
X _ {52} &= xxxxxxxxxByyyyyyyy, \\
X _ {53} &= xxxxxxxxxaByyyyyyyy, \\
X _ {54} &= xxxxxxxxxbaByyyyyyyy, \\
X _ {55} &= xxxxxxxxxbyyyyyyyyy, \\
X _ {56} &= xxxxxxxxxbAyyyyyyyyy, \\
X _ {57} &= xxxxxxxxxbAByyyyyyyyy, \\
X _ {58} &= xxxxxxxxxxByyyyyyyyy, \\
X _ {59} &= xxxxxxxxxxaByyyyyyyyy, \\
X _ {60} &= xxxxxxxxxxbaByyyyyyyyy, \\
X _ {61} &= xxxxxxxxxxbyyyyyyyyyy, \\
X _ {62} &= xxxxxxxxxxbAyyyyyyyyyy, \\
X _ {63} &= xxxxxxxxxxbAByyyyyyyyyy, \\
X _ {64} &= xxxxxxxxxxxByyyyyyyyyy, \\
X _ {65} &= xxxxxxxxxxxaByyyyyyyyyy, \\
X _ {66} &= xxxxxxxxxxxbaByyyyyyyyyy, \\
X _ {67} &= xxxxxxxxxxxbyyyyyyyyyyy, \\
X _ {68} &= xxxxxxxxxxxbAyyyyyyyyyyy, \\
X _ {69} &= \dots.
\end{align}
\]
特に、 $n \in \mathbb{N}$ に対し、
\[
\begin{align}
X _ {6n + 1} = x^n b y^n, \\
X _ {6n + 2} = x^n bA y^n
\end{align}
\]
が従うのがみて取れる。よってこれを実装すればよろしい。
ポイント
規則性があるはずだと信じて実験し続ける力と、それでもダメならプログラムを書いて大きなものを見てみようという力が両方必要な問題だと思った。
E - Snuke the Phantom Thief
解答
$0$-indexed とする。盗む宝石の数 $K$ の数を全探索することにする。これを fix する。
まず $x$ 座標だけを考慮する。盗む $K$ 個の宝石の $x$ 座標が昇順に並べてみる。この状況で、条件をみると、以下のように解釈できる。
- $(``L”, a, b)$ とは、 $x$ 座標が $a$ 以下であるものは $0$ から $b - 1$ 番目の宝石までに限られることを意味する。つまり、 $b$ 以上 $K$ 未満番目の宝石の $x$ 座標は $a$ より大きくないといけない。
- $(``R”, a, b)$ とは、 $x$ 座標が $a$ 以上であるものは $K - b$ から $K - 1$ 番目の宝石までに限られることを意味する。つまり、 $0$ 以上 $K - b$ 未満番目の宝石の $x$ 座標は $a$ より小さくないといけない。
これにより、 $i$ 番目の宝石が充たすべき $x$ 座標の区間が $(l _ i, r _ i)$ のように決まる。同様なことが $y$ 座標にも言える。
宝石の価値の和を最大化するためには、最小費用流を使えばよろしい。
実装
まず頂点を決める。 $C = 10^{15} + 10$ とする。
- 頂点 $400$: スタート地点、
- 頂点 $i$: $i$ 番目の $x$ 座標の「区間」に相当する点、
- 頂点 $100 + i$, $200 + i$: 宝石 $i$ に相当する点、
- 頂点 $300 + i$: $i$ 番目の $y$ 座標の「区間」に相当する点、
- 頂点 $401$: ゴール地点。
次の規則で辺を張る。全て容量 $1$ であり、費用を書かなかった場合は費用 $0$ である。
- 全ての $0 \leq i < K$ に対し $400 \to i$ を張る。
- 全ての $0 \leq i < K$, $0 \leq j < N$ に対し、 $i$ 番目の $x$ 座標の区間に宝石 $j$ が含まれていたら $i \to 100 + j$ を張る。
- 全ての $0 \leq j < N$ に対し、 $j$ 番目の宝石の価値 $v _ j$ に対し、費用 $(C - v _ j)$ の辺 $100 + j \to 200 + j$ を張る。
- 全ての $0 \leq i < K$, $0 \leq j < N$ に対し、 $i$ 番目の $y$ 座標の区間に宝石 $j$ が含まれていたら $200 + j \to 300 + i$ を張る。
- 全ての $0 \leq i < K$ に対し $300 + i \to 401$ を張る。
あとは最小費用流 $X$ をダイクストラ法+ポテンシャル法を用いて求める。すると答えは $CK - X$ である。これを全ての $1 \leq K \leq N$ について行えばよろしい。
計算量
まず $K$ の種類が $N$ 個ある。頂点 $O(N)$ 個、辺の数は $O(N^2)$ 個なので、ダイクストラ法を一度行うと $O(N \log N)$ の計算量である。最小費用流の計算にかかる回数は最悪で $O(N)$ かかる。よって全体の計算量はおおよそ $O(N^3 \log N)$ であろう。十分間に合う。
ポイント
観賞用の問題。今の実力では解けないけれども、納得することはできる。
