AtCoder Regular Contest 102
Updated:
Source codes
Solutions
C - Triangular Relationship
すぐにわかることとして、 $2a, 2b, 2c$ がいずれも $K$ の倍数でなければならない。
仮に $K$ が $2$ の倍数でなければ、この条件は $a, b, c$ がいずれも $K$ の倍数であることと同値である。これが十分であるのはすぐわかるし、数え方も容易である。
仮に $K$ が $2$ の倍数であれば、この条件は $a, b, c$ がいずれも $K / 2$ の倍数であることと同値である。そこで、例えば $a = n (K/2)$, $b = m (K/2)$ としてみると、 $a + b = (n + m) K / 2$ となる。これが $K$ の倍数であるための必要十分条件は $(n + m) / 2$ が整数であることである。つまり $a, b, c$ を $K/2$ で割ったときの商が偶数・奇数かが一致している必要があり、以上で必要十分条件である。数え方であるが、 $i = 1, \dots, N$ のうち、 $i$ が $K/2$ の倍数である際に $i/(K/2)$ が偶数ならば cnt[0]++; とし、奇数ならば cnt[1]++; とする。あとはそれぞれ $3$ 乗して足すと答えになる。
ポイント
必要条件を書き出していったら十分条件だった のパターン。
D - All Your Paths are Different Lengths
$0$-indexed とする。仮に $L = 2^K$ であれば、 $N = K$ として、 $i = 0, \dots, K - 2$ に対し、 $i$ から $i + 1$ へ長さ $0$ の辺と長さ $2^i$ の辺を張れば良い。こうすれば $i = 0, \dots, L-1$ の各桁において立っているところだけ $2^j$ の辺を通っていけば実現可能である。
問題は $2^K \leq L < 2^{K+1}$ の場合である。上記のことを実行したあと、 $2^K \leq i < L$ の長さの辺を実現する必要がある。下流の方が使いやすいので、 $i$ から $N-1$ へ何らかの辺を張ることにする。すると、 $i = 0, \dots, N - 2$ に対して、 $L$ の $i$ ビット目が立っている場合に $L$ の $i$ ビット以下を全て折った数を cost として持たせた辺を張ればよろしい。
以下の画像は $L = 11 = 1011_{(2)}$ の場合である。実際に解いた時のメモである。
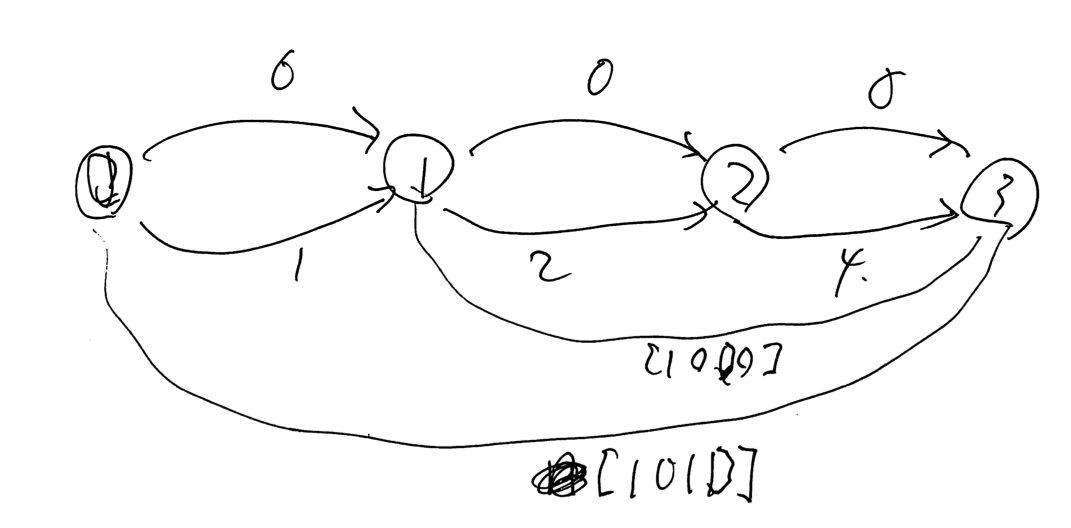
ポイント
何となくとビット演算だろうなーと思ってサクッと思いついた。 $L = 8, 9, 10, 11$ を試して大丈夫そうだなと思った。一発で通って良かった。先に void flush(); と void add_edge(int x, int y, int w); を作っておいたのでバグなく実装できたような気がする。
E - Stop. Otherwise…
包除原理を用いればできそうだけどうまく考えがまとまらなかった。
解説を聞いて理解した。もっと時間あればできたかもしれないけど、自分の考え方が混沌としているのがよくないと思った。
