AtCoder Grand Contest 026
Updated:
ABCD は完成。 E は完了はしていないが AC はした。
今日は ABC はクリアして、 D はできませんでした。 D ができたら最高だったが、 BC が両方取れたのならまぁまぁ調子は良かったのではないかと思う。
Source codes
Solutions
A - Colorful Slimes 2
コンテスト中に思いついた解法
貪欲法。前の方から見ていって、必要なら奥の方の色を変える方がよろしい。その色は前後の色のどちらでもなければ何色でも同じであるから、例えば色 $20000$ に変更すればよろしい。
模範解答
まず色が全て一致している場合を考察する。この場合その長さを $N$ とすると答えは $N/2$ である(計算機の除算)。次に色がバラバラである場合を考察すると、色の変わり目で問題を分けて良いので、その和が答えになる。
コメント
模範解答の方が難しいと思う。切れ目で separate するのが難しい。
while !a.empty?
sep = false
for i in 0...a.size
if a[i] != a[i+1]
ary << a[0..i]
a = a[i+1..-1]
sep = true
break
end
end
if !sep
ary << a
a = []
end
end
B - rng_10s
コンテスト中に思いついた解法
まず自明な場合を排除しよう。 $A < B$ の場合はそもそも最初の日にジュースを買えないから No である。 $B > D$ の場合も需要より供給が少ないので永遠にジュースを買い続けることはできない。ゆえに No である。また以上の場合でなく、かつ、 $A \leq C$ ならば、 $1$ 日目の翌日に必ず補充され、しかも在庫はさらに大きくなる一方であるから、答えは Yes である。以下これらは排除した状態で検討する。
ジュースを買えない瞬間というのは、どういうことが起きているか検討する。 $m$ 回目の商品補充を終えると $A + Dm$ 個のジュースを累計で並べたことになる。ここで $n$ 回目まではジュースが買え、 $(n+1)$ 回目はジュースが買えないためには、その間で補充が行われないのだから、その必要十分条件は、 $A + Dm - Bn > C$ かつ $A + Dm - B(n+1) < 0$ である。これを変形すると $A - B + Dm < Bn < A - C + Dm$ となる。つまり求める条件は
\[
(\exists m, n \in \mathbb{N})(A - B + Dm < Bn < A - C + Dm) \tag{B.1}
\]
である。ここでまず $A, B, C, D$ は互いに素であるとして良い。そうでなければ最大公約数で割っても同じ条件であるからである(実はこの動作は必要ないのだが)。続けて $X = A - B$, $Y = A - C$ とする。すると (B.1) 式の「中身」は $X + Dm < Bn < Y + Dm$ となる。ここで左辺 $X + Dm$ の $B$ による剰余(ここでは普通に $0, \dots, B-1$ のいずれかとする)に着目する。 大きければ大きいほど 、この不等式を充たす $n \in \mathbb{N}$ は存在しやすくなる。ではその最大値はいくつだろうか。まず、 $Dm \in \mathbb{Z}/B\mathbb{Z}$ の自然な全射で考えると $0, g, 2g, \dots, B-g$ の任意の値を取りうるし、それ以外は取れない。 $X$ の寄与を考えると、これらから $X$ だけずれる。つまり $X, g + X, 2g + X, \dots, B-g + X$ なのだが、実際は剰余を取っているので、最大値は $B - g + X \% g$ である。左辺と右辺の差は $Y - X$ であるので、結局 $g - X \% g < Y - X$ が (B.1) の必要十分条件である。これを見て Yes or No を出力する。
模範解答
やっていることはほぼ同じ。発想の仕方が違うので共有しておきたい。
夜の時点での在庫に着目する。 $x$ を夜の時点での在庫(ただし負の数も許す)とし、 $f(x)$ をその次の夜の時点での在庫とする。すると、
\[
f(x) =
\begin{cases}
x - (B - D) & (x \leq C), \
x - B & (x > C)
\end{cases}
\]
が成立する。そこで $f^{(n)} = f \circ \dots \circ f$ のようにしたときどうなるか考察する。これは $1$ 次元における離散的な力学系になっているが、今回の場合まず $B - D \geq 0$ が必要である。そうでなければ負の方向に発散する。 $B - D \geq 0$ の場合、発散せずある領域上の周期運動に収束する。図にすると解説放送の通りである。区間 $I = [C - B, C + D - B]$ の中に入ったら出てこない。そこでこの区間内で取りうる値の最小値 $y$ を求めることになる。求める条件は $\min(A - B, y) \geq 0$ である。 $f$ は $I$ 上で mod $D$ で考察すると $-B$ をしている。区間の長さも $D$ であるから、上と同じような考えをして $y = C - B + (A - B)\%g$ である。

ポイント
最初は $D$ の寄与がよくわからなかった。その後は $X + Dm$ の $B$ による 剰余の最大値 を考えることができ、クリアできた。取り得る値を考察するのは群論とかやっていれば楽勝なのでなんとかなる。
C - String Coloring
正しい色分けをした時に、文字を前半と後半で区切って、後半だけ反転させる。前半の赤・青文字を普通に読んだ文字列を $(A, B)$ 、後半の反転の赤・青文字を普通に読んだ文字列を $(A’, B’)$ とすると、 $(A, B) = (B’, A’)$ が成立する。これが条件を充たす必要十分条件である。
そこで $S$ の前半を改めて $S$ とおき、後半の反転を $T$ とおく。すると $(A’, B’)$ の型を typedef tuple<string, string> P; として、 $(A’, B’)$ をすべて列挙して map<P, ll> M; の中に数えておく。 $(A’, B’)$ の順序は保持しておく。つまり逆は一般に区別する。続けて $(A, B)$ を全部列挙して、 M に問い合わせる。答えを足す。これだけ。計算量は $O(N 2^N \log(2^N)) = O(N^2 2^N)$ であり、 $N = 18$ なら間に合うだろう。
ポイント
見た瞬間に半分全列挙を思いついたのが功を奏した。順序を保持するところを間違えていた。あと $T$ ではなく反転しない文字列を考えていて答えが出ていなかった。
類題を知っていたので、逆に読んだりするのはそこまで苦ではなかった。
D - Histogram Coloring
色は黒白とする。 $0$-indexed とする。
まず考察。十分広い長方形を塗ろう。このとき、一番下の段が決まってしまうと、その上の段の塗り方は 例外を除いて ほぼ決まってしまう。真下と逆の色で塗るしかないからである。例えば BWBWW の上の段は WBWBB 以外ありえない。最初を B で塗ろうとしても最後で行き詰まる。しかし 例外が存在する 。それは完全に互い違いに B と W が塗られている場合である。これは上の段は 2 パターンあって、逆で塗るか全く同じで塗るかである。これはその上の段も、さらにその上の段もそうなる。
そこで、ヒストグラム $H$ に対して、以下の通りに $f, g$ を定義する。
$f(H) =$ 条件を充しながら $H$ を塗る全ての場合の数
$g(H) =$ 条件を充しながら $H$ を塗る方法のうち、一番下の段が互い違いになっているものであり、かつ、左下が黒であるものの場合の数 (「白」の場合の数も全く同じことに注意)
ヒストグラムをどのように持つかは後で議論する。また、 $h(H)$ を $H$ の最小の高さとする。ここで DFS で $f(H), g(H)$ を求める。まず初期条件として、マスが 1 マスの場合は、 $f(H) = 2$, $g(H) = 1$ であり、 $H = \emptyset$ の場合は $f(H) = g(H) = 1$ である。以下場合わけをする。
$h(H) \geq 2$ のとき: $H$ の下の $h(H) - 1$ マスを切り取ったヒストグラムを $H’$ とする。下図参照。
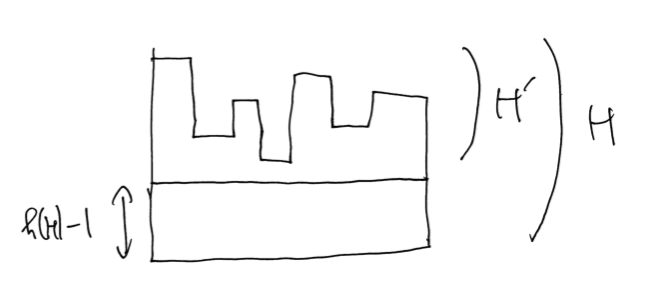
互い違いでないもの $f(H’) - 2g(H’)$ と、互い違いのもの $2g(H’)$ を分けて数えて、場合の数は以下の通りになる。
\[
\begin{align}
f(H) &= f(H’) - 2g(H’) + 2 g(H) \cdot 2^{h(H) - 1} \
&= f(H’) - 2g(H’) + 2^{h(H)} g(H), \
g(H) &= 2 g(H) \cdot 2^{h(H) - 2} \
&= 2^{h(H) - 1} g(H).
\end{align}
\]
$h(H) = 1$ のとき: $h(H) = 1$ を実現するマスで左右にわける。それぞれ $H_1, H_2$ とする。
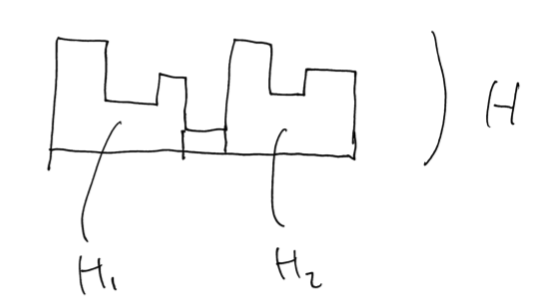
場合の数は普通に求まる。
\[
\begin{align}
f(H) &= 2 f(H_1) f(H_2), \
g(H) &= g(H_1) g(H_2).
\end{align}
\]
以上を踏まえて、ヒストグラムの持ち方は、区間 $[l, r)$ と下からどれだけ切り取ったか $h$ を持っておけばよろしい。
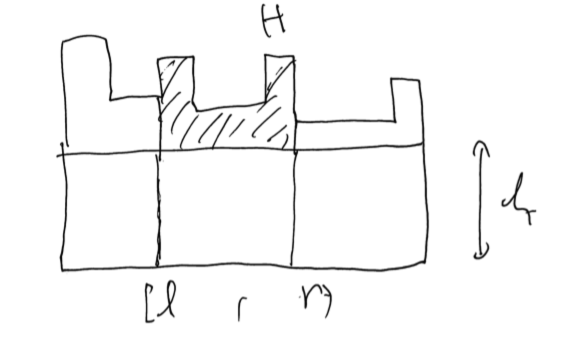
$h(H)$ に関しては素朴に $O(N)$ で求めてよろしい。 typedef tuple<ll, ll> P; で $(f, g)$ の組を同時に求める関数 P func(int l, int r, ll h); を定義する。答えは get<0>(func(0, N, 0)) である。計算量は $O(N^3)$ である。
ポイント
縦に塗ることばかり考えていた。横に塗るのは気がつかず。考察ミスをしていた。
例えば
BWBWWの上の段はWBWBB以外ありえない。最初をBで塗ろうとしても最後で行き詰まる。
この部分の気付かず、多すぎる値を出力していた。その他の大筋の考察は正解だった。もう少しでできそう。
E - Synchronized Subsequence
実装自体はむしろ易しいのだが、なぜそれで良いかと言われると非常に難しい。実装は最初に書いておき、その後その正当性を証明しよう。
解答
$a$ に $+1$ 、 $b$ に $-1$ を振り、累積和が $0$ になる空でない disjoint な部分列にできるだけ多く分割する。この部分列を 正規部分列 と呼ぶ。このうち $a$ から始まるものを a 型と呼び、 $b$ から始まるものを b 型と呼ぶ。それぞれの正規部分列からは最大の部分列を以下の手順で取り出す。
- a 型の正規部分列からは $ababab \dots ab$ の形の最長の部分列を貪欲に取り出す。
- b 型の正規部分列は、候補が複数ある。「 $i$ 番目以降の $b, a$ を全て取り出す」を全ての $i$ に対してやり部分列を比較し、最大のものを取り出す。ここは $O(N^2)$ でよい。
このようにしてできた最大部分列を後ろから繋げることを検討する。その文字を前につなげて大きくなるのであれば前に繋げる。これを貪欲に繰り返す。最後にできた文字が答え。
解答の正当性
解答は非自明なことだらけである。順番に検討する。正規部分列で $i$ 番目に出てくる $a, b$ をそれぞれ $a_i, b_i$ とおく。部分列とかいたら、すべて、条件を充たす部分列である。
補題 1: a 型の正規部分列では、任意の $i$ に対し $a_i$ は $b_i$ より前に出てくる。 b 型の正規部分列では、任意の $i$ に対し $b_i$ は $a_i$ より前に出てくる。
証明:逆に出てくるならば、その前で正規部分列は切れているはずであるからである。
しばらく、正規部分列の部分列から最大の部分列を取る方法を議論する。
補題 2: a 型の正規部分列の部分列で、ある場所で $b$ が隣り合うならば、その前に $a$ が隣り合う場所がある。
証明: $i < j$ が存在し、 $S$ のある地点で $b_i b_j$ が隣り合ったとする。すると補題 1 より、それ以前に $a_i$ と $a_j$ が $S$ に含まれている。この 2 つが隣り合っていれば主張は成立する。そこで実際は隣り合っていないと仮定する。 $k < i < j$ が存在して、 $a_i, b_k, a_j$ の順番で出てくる。すると $a_k, a_i$ について同じようなことが起こる。$(i, j) \mapsto (k, i)$ の降下は有限回であるので、どこかでストップする。すなわち、 $a$ が隣り合う場所がある。
補題 3: a 型の正規部分列の最大の部分列 $S$ は $ababab \dots ab$ の形の最長の部分列である。
証明:補題 1 より、全ての部分列は $a$ から始まることに注意されたい。この形でないものが最大であると仮定する。 $bb$ と隣り合うか $aa$ と隣り合うかであるが、補題 2 より、前者の場合も後者がおきているので、後者だけを検討すればよろしい。さて $i < j$ が存在し、 $S$ で $a_i a_j$ が隣り合っていると仮定しよう。すると、補題 1 より、 \[ S = a_0 \dots a_i a_j (x \dots x) b_i \dots b_j \dots \] となっているが、ここから $a_j$ と $b_j$ を取り出して他の場所をそのままにした \[ S’ = a_0 \dots a_i (x \dots x) b_i \dots \dots \] は、 $S < S’$ を充たす。なぜなら、 $(x \dots x)$ の部分で初めて $b$ が現れる場所が $S’$ の方が早くなるので、辞書順で大きくなるからである。仮にここに $b$ が含まれなかったとしても、 $b_i$ で同じことがいえる。これは $S$ の最大性に反する。よって最大の部分列は $ab$ がずっと続く形しかありえない。そのうち最長のものが最大である。ゆえに示された。
補題 4: b 型の正規部分列の最大の部分列 $S$ に、ある $i$ が存在し $a_i, b_i$ は両方組み込まれていると仮定する。すると $a_{i+1}, b_{i+1}$ も組み込まれている。
証明:補題 3 と同様に考察する。場合分けをする。まず \[ T = b_0 \dots b_i \dots b_{i+1} (x \dots x) a_i \dots a_{i+1} \dots \] を検討する。これから $b_{i+1}, a_{i+1}$ を削除した \[ T’ = b_0 \dots b_i \dots (x \dots x) a_i \dots \dots \] とを比較すると、 $T > T’$ が成立する。 $(x \dots x)$ の部分で初めて $a$ が出てくる場所が前になるからである。先ほどと同様である。 \[ T = b_0 \dots b_i \dots a_i \dots b_{i+1} (x \dots x) a_{i+1} \dots \] も同様である。これで示された。
疲れてきた。補題 5 以降はまた今度。
ポイント
F - Manju Game
ポイント
Others
A - sample: 4, tle: 2.000, time: 03:08, from_submit: 86:04
B - sample: 2, tle: 2.000, time: 50:09, from_submit: 35:56
C - sample: 4, tle: 3.000, time: 35:56, from_submit: 00:00
D - sample: 4, tle: 2.000, time: 00:00
E - sample: 4, tle: 2.000, time: 00:00
F - sample: 3, tle: 2.000, time: 00:00
案外 B の方が苦労している。
