AtCoder Grand Contest 021
Updated:
Source codes
Solutions
A - Digit Sum 2
まずそれ自身が答えの可能性がある。例えば $N = 2$, $N = 19$ など。解を与える数字は、先頭に小さい数を持ってきた方が、考察しやすく「有利」である。例えばサンプルでは $N = 9995$ の解を与える数字を $9989$ と解説しているが、実際は $8999$ でも構わない。つまり答えとなる数字の候補は、先頭 $1$ 桁目を $1$ 減らしてあとは $9$ を埋めた数字である。この $2$ つの max を出力する。
ポイント
ここからして間違えているから冴えてない。
解説放送の方が冴えている考察だった。たとえば $N = 39345$ だと 5 桁目は $3$ 以下、 4 桁目は $9$ 以下である。よって最大を与える候補は $39999$ である。これが $N$ と等しければそれが最大。そうでなければ最大桁を減らした $29999$ は必ず $N$ 以下であるからこれが最大を与える。 桁ごとに上から抑える のがポイントである。
B - Holes
まず $N$ 頂点の凸包を作る。プログラミングコンテスト p.234 - 235 を参照。凸包の内部(や辺の上)に乗っている点は確率 $0$ である。というのも凸包の外の領域が広すぎて、その点が最小点である領域は小さすぎるからだ。つまり最小距離を与える領域が有界であるような点は確率 $0$ を出力することになる。したがって、凸包の頂点での確率を求めることに帰着される。
まず $3$ 点で考察してみよう。この場合、全領域 $\mathbb{R}^2$ は外心を中心とした各辺への垂直二等分線を半直線へ延長して分割した $3$ つの領域に分かれる。その面積は無限大だが、実際は ${ x^2 + y^2 \leq R^2 }$ との共有部分の面積だから有限の値である。その比率は、外心を中心とした角度の比率にほぼ等しい( $R = 10^{10^{10}}$ は大きすぎるから)。仮に点 $A$ の角度を $\alpha$ とすると $(\pi - \alpha) / 2\pi$ が確率である。
$4$ 点以上でもほぼ同じである。隣り合う $2$ つの点だけが遠方でしか影響を及ぼさないので、結局 $i$ 番目の点 $A_i$ での確率は、 $\alpha_i = \angle A_{i-1}A_iA_{i+1}$ とすると $(\pi - \alpha_i) / 2\pi$ である。ここで、 \[ \sum_{i = 0}^{M-1} (\pi - \alpha_i) = M \pi - \sum_{i = 0}^{M-1} \alpha_i = 2\pi \] であることに注意した。
もう少ししっかり証明を書くべきだけど「有界領域の差は関係ない」を使うだけでできる。
ポイント
上記の解答は $N = 2$ を含む。
これは素早く解答を思いついたが、実装に手間取った。順位的にはどうなんだろうか。
C - Tiling
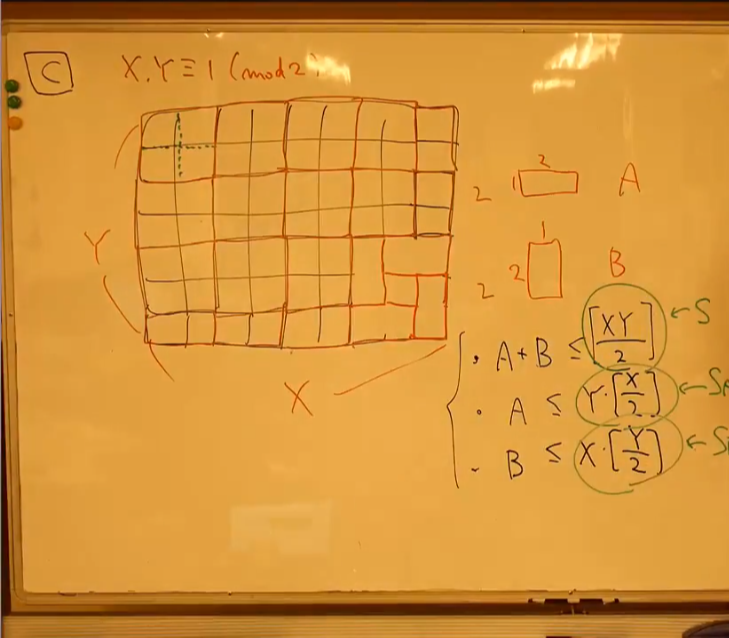
この問題では、割り算は全て整数の余り算とする。$X = N$, $Y = M$ とする。$1 \times 2$ のタイルをタイル $a$ と呼び、 $2 \times 1$ のタイルをタイル $b$ と呼ぶ。 $2 \times 2$ の正方形のことを単に正方形と呼ぶ。
まず自明な条件というのがある。面積から、 $A+B \leq (XY)/2 = S$ である。また、 $A$ と $B$ にも限界がある。 $A \leq X(Y/2) = S_A$, $B \leq (X/2)Y = S_B$ である。さらに $A, B \geq 0$ である。これらの条件は以下では前提とし本質的でない注釈を省く。
左上から $2 \times 2$ に区切って、残りをタイル $a, b$ で埋め尽くす。仮に正方形を全てタイル $a$ で埋め尽くすと、 $A + B = S$, $A = S_A$ が達成される。この状態から順番に $1$ つの正方形を $a$ から $b$ に変更することにより、$(A, B)$ の点が YES ならば $(A-2, B+2)$ が YES となる。また $(A, B)$ が YES ならば任意の $(A’, B’) \leq (A, B)$ も YES となる。ここで順序は標準順序。
ここまでを $(A, B)$ 平面上で図にする と、以下の通り。 以下の画像は解説放送から引用しています。
残る点は、例えば $(S_A - 1, S - S_A + 1)$ などの 限界から奇数だけずれた点(緑色の点) である。この場合は「$X, Y$ がどちらも奇数の場合」と「$XY$ が偶数の場合」によって結論が違う。前者は YES で後者は NO となる。
まず「$X, Y$ がどちらも奇数の場合」を検討しよう。以下のように右下の $3 \times 3$ のマス目を次図のように区切ることで、 $(A, B)$ が YES ならば $(A \pm 1, B \mp 1)$ が YES となる。
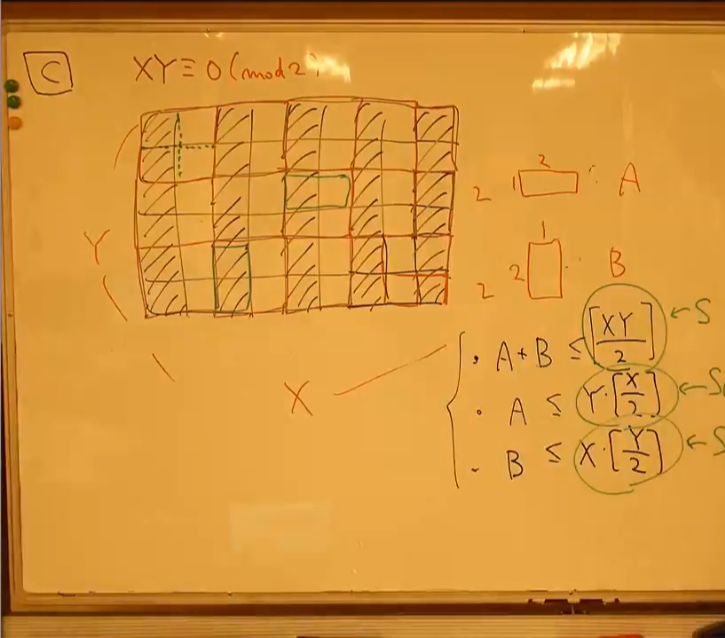
「$XY$ が偶数の場合」の場合、以下のように縞模様に塗る。すると、最密充填の際の $A$ または $B$ の偶数奇数が決まる。ゆえに $(S_A - 1, S - S_A + 1)$ などは全部できない。
ポイント
C か D を解くのに 40 分しか使えなかったので考察はできなかっただろう。まず $(A, B)$平面上の点で考察する ところができない。これは定跡であるのに…またそこを乗り越えても、 $3 \times 3$ は最初から頭にあったけど、縞模様は無理だろう。しかし問題文の性質を鑑みてえいやといって提出できたかもしれない。そこが YES だと自明な条件だけで足りてしまうからである。
実装でミスったところ: $X, Y$ が奇数の時は、正方形から敷き詰めるのではなく、端から敷き詰める。そのあと正方形を敷き詰める。こうしないと入らなくなる場合がある。
D - Reversed LCS
やったこと
普通の LCS は動的計画法で求まるのはすぐわかるんだけど、そのさきはどうすればいいのやら、解答が $\min(\lvert S \rvert, \mathrm{LCS}(S, S’) + 2K)$ で抑えられるのはわかるんだけどこれを提出したら WA だった。
睡眠導入剤飲んで寝ます。復習は明日。
解説放送
次の事実を証明する。
補題 :文字列 $T$ の逆を $T’$ とする。このとき $l = \mathrm{LCS}(T, T’)$ は $T$ の部分列のうち回文であるものの長さの最大値 $l_0$ と一致する。
例がないとやりづらいので、 $T = cbcabcabc$ とする。
まず $l_0 \leq l$ を示す。 $T$ の部分文字列の最長回文の具体的な構成の 1 つは $cbababc$ である。すると、 $T$ のリバースである $T’$ にも、 部分文字列として全く同じ最長回文 $cbababc$ も含まれている ことになる。すなわち、 $T$ の部分文字列の最長回文は、 $T, T’$ の共通部分文字列である。ゆえに、 $l_0 \leq l$ である。
次に $l_0 \geq l$ を示す。 $\mathrm{LCS}(T, T’)$ の具体的構成の 1 つは $cbabcbc$ である。これを前から後ろから $T$ 上で 1-indexed でナンバリングしていくと、$cbca[b]cabc$ の $[b]$ で $4$ で交差していることがわかる。この交差しているところで、「乗り換え」をすると、そこからちょうどナンバリングを逆にたどることになるので、回文ができる。逆も同じなので、回文が 2 つできる。長さをそれぞれ $l_1, l_2$ とする。ナンバリングの総数を数えると $l_1 + l_2 = 2l$ を充している。 $l_0 \geq \max(l_1, l_2) \geq l$ である。
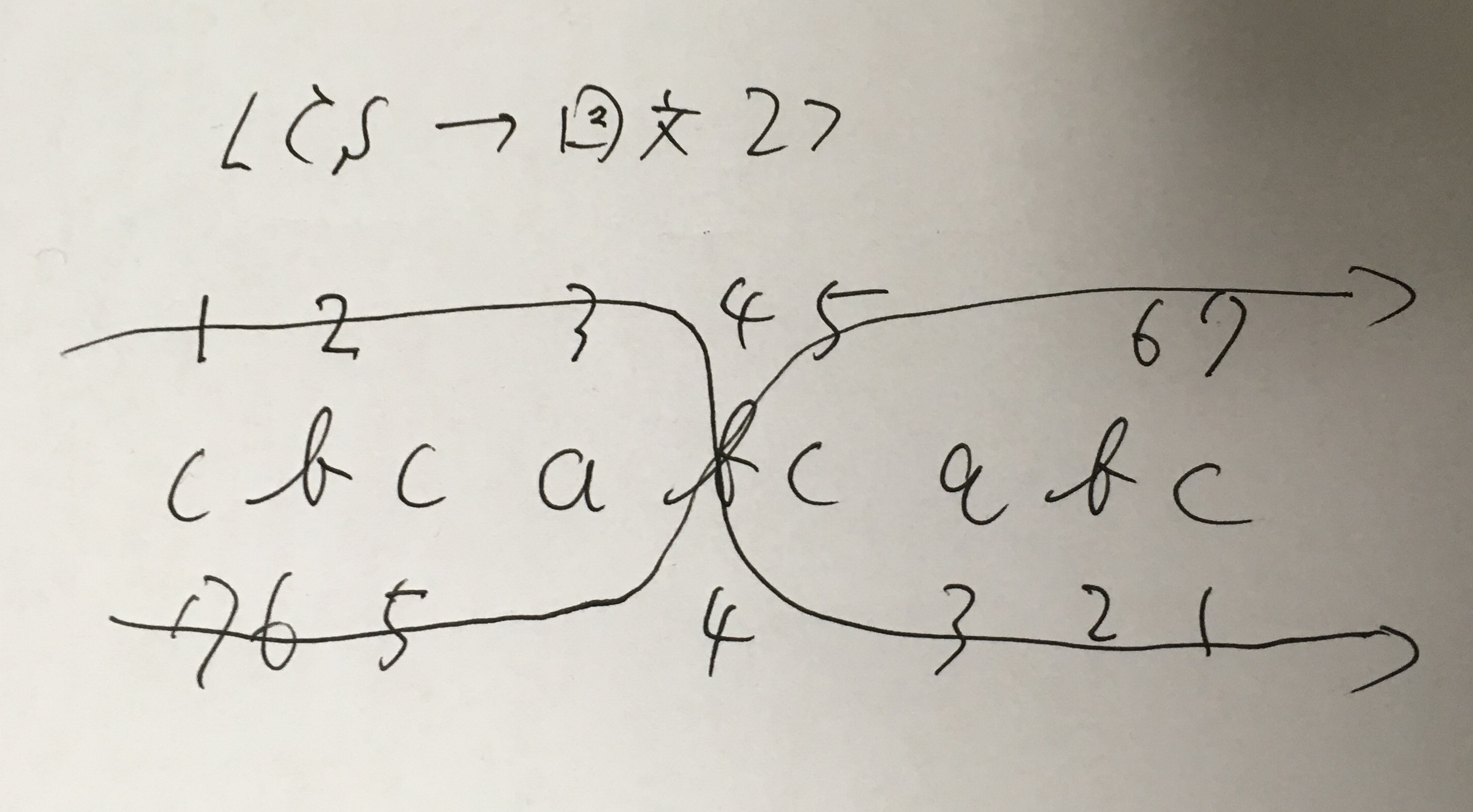
以上より $l = l_0$ である。証明終わり。
あとは
$DP[l][r][k] = $ $S$ の部分文字列 $S[l, r)$ を $k$ 箇所変更した時の部分列の最長回文の長さ
として区間 DP をする。ここで解説放送が終わった。
DP の部分の実装
自分の実装が理想的なのかどうかはわからないけれども、自分の解法を書く。メモ化で書く。 $S_i$ を $S$ の $i$ 番目の文字とする。
あとで使う下準備をしておく。
$DP2[i][c] = $ 接尾語 $S[i, \dots)$ で先頭からみて一番最初に文字 $c$ が出てくる場所
と定義する。元の文字列の位置で持っておく。これは後ろから DP すればすぐにできる。
まず $r - l \leq 2k + 1$ ならば $DP[l][r][k] = r - l$ である。問答無用で前半を後半に合わせてしまえば全体が回文となるためである。 $r = l$ のような自明なケースもここに入っている。
この状態で $DP[l][r][k]$ がまだ求まっていないときに、これを求める方法を考察する。遷移の方法は 3 通りある。その max をとる。
- $S_{r-1}$ を変更する場合
- $S_{r-1}$ を変更せず、回文に使用しない場合
- $S_{r-1}$ を変更せず、回文に使用する場合
まず 1 番目は簡単で、変更するなら $S_l = S_{r-1}$ とするのが一番得をする。つまり $DP[l+1][r-1][k-1] + 2$ である。 2 番目も簡単で、 $DP[l][r-1][k]$ である。
3 番目はどうだろうか。 $S_l$ やそれ以降の文字を変更することが頭に過ぎるが、これは結局最後の文字を変更する動作とコスト・結果が変わらない。だから変更については考える必要がない。 $S_l$ から順に見ていって $S_{r-1}$ と同じ文字が出てくるまで待つのが、漏れているケースのうちの最善ということになる。ゆえに $DP[DP2[l][S_{r-1}] + 1][r-1][k] + 2$ である。
以上の max をとる。計算量は $O(26N + N^2 K)$ である。 DP なら余裕だし、後ろの項は原理的に「限界」までいかないのでメモ化で十分のはず。
追記
3 番目は「$S_{r-1} = S_l$ なら $DP[l+1][r-1][k] + 2$ 、一致していないなら $DP[l+1][r][k]$」でいいという。再帰していけば $DP[DP2[l][S_{r-1}] + 1][r-1][k] + 2$ に合流する。参考:くれなゐの雑記 AGC021 D - Reversed LCS
回文を経由せず直接漸化式を立てる方法もあるという。参考:kmjp’s blog AtCoder AGC #021 : D - Reversed LCS
ポイント
私のような凡人が「$T$ の部分列の回文は、 $T$ と $T’$ の共通部分列」を先に思い付けば、怪しい実装ながらたどり着けた可能性はあるけども、 40 分では無理です。解説放送の rng さんは最長共通部分列から回文を作る方法を先に提示していたので、天才はそっちから思いつくのかなとしんみりしていた。
E - Ball Eat Chameleons
解説 PDF が充実しているので、ほとんどそれの写しになる。
本解答
投げ入れるボールの数を、赤を $R$ 個、青を $B$ 個とし、固定する。$R+B = K$ を充す $(R, B)$ 全てに対して、条件を充す列を求める。 $N > K$ の時は答えは $0$ である。よって以下では $N \leq K$ とする。
最終的にあるカメレオンが赤色であるための必要十分条件は、以下の 1., 2. のいずれかを充すことである。
- 赤色のボールを青色よりも多く食べている。
- 赤色と青色のボールを同数食べ、かつ、最後に食べたボールが青色である。
$R < B$ のとき、条件を充す列は存在しない。
$R = B$ のとき。全てのカメレオンは 2. の条件を充すしかない。 disjoint な部分列であって (赤, 青) であるものが $N$ 個取れる必要がある。これは前から貪欲に取っていけばよろしい。さらに最後は青でないといけない。逆にこれを充していれば、余計なボールを全て最後のボールを食べるカメレオンに食べさせればよろしい。この条件を $(R, B)$ を座標とする $2$ 次元座標系で考察すると
$y - x \geq R - N + 1$ を通らないで $(0, 0)$ から $(R, B-1)$ へ至る経路の個数
となる。
$0 < B-R < N$ のとき。ほぼ同様である。 1. を充すカメレオンが必ずいる。 disjoint な部分列であって (赤, 青) であるものが $N$ 個取れる必要がある。これは前から貪欲に取っていけばよろしい。逆にこれを充していれば、余計なボールを全て 1. を充すカメレオンに食べさせればよろしい。結局、
$y - x \geq R - N + 1$ を通らないで $(0, 0)$ から $(R, B)$ へ至る経路の個数
$B-R \geq N$ のとき。全てのカメレオンを 1. で充すことができる。全ての列は条件を充す。
あとは カタラン数の拡張 の知識があれば解ける。
カタラン数の拡張
補題:「$y - x \geq T$ を通らないで $(0, 0)$ から $(X, Y)$ へ至る経路の個数」は、「$(0, 0)$ から $(X, Y)$ へ至る経路の個数」から「$(0, 0)$ から $(Y-T, T+X)$ へ至る経路の個数」を引いたものである。すなわち、以下で求まる。 \[ \begin{pmatrix} X+Y \\ X \end{pmatrix} - \begin{pmatrix} X+Y \\ Y-T \end{pmatrix} \]
証明:まず何も考えず、
$(0, 0)$ から $(X, Y)$ へ至る経路の個数
は $\begin{pmatrix} X+Y \\ X \end{pmatrix}$ である。この中から、
$y - x \geq T$ を一度必ず通って $(0, 0)$ から $(X, Y)$ へ至る経路の個数
を引くことを考察する。この数は次のトリックで求められる。このような経路を 1 つ固定する。 この経路で $y - x = T$ に「初めてタッチした」部分から先を $y - x = T$ を対象に折り返す と、$(0, 0)$ から $(Y - T, T + X)$ への経路を 1 つ与えていることになる。逆に $(0, 0)$ から $(Y - T, T + X)$ への経路は、初めて $y - x = T$ にタッチした場所から折り返すと $y - x \geq T$ を一度必ず通って $(X, Y)$ への経路となる。この 2 つは $1 : 1$ 対応しているので、結局、
$(0, 0)$ から $(Y-T, T+X)$ へ至る経路の個数
に等しく、 $\begin{pmatrix} X+Y \\ Y-T \end{pmatrix}$ である。だから以上のようになる。終わり。
ちなみに 一般のカタラン数 は、 $X = Y = n$, $T = 1$ の場合である。すなわち
\[ C_n = \begin{pmatrix} 2n \\ n \end{pmatrix} - \begin{pmatrix} 2n \\ n-1 \end{pmatrix} \]
と定義される。
ポイント
実装自体は難しくはないのだが、絶対解けない。
F - Trinity
ポイント
Others
復習は手早く済ませて、かつ、見返したときに「そうそうあれあれ」となりたいので、 解説放送のスクショを引用する ことにしました。今後もそうしたいと思っています。
出典も明記しています。また、解説している方 (rng さん、 snuke さん、 chokudai さん、その他の方々) の肖像権を侵害しないようにします。 それでも万が一 AtCoder 社から差し止めを申し立てられた場合は削除します。
冷静に振り返ると、今回は A, B を取ったのが限界で、 C, D はいずれも取れなかっただろうと推測できる。だから最善をやったと理解している。定跡と発想のトリガーを学び、今後生かしていく。
今回はレーティングが 1 だけ上がった。レーティングに見合った内容だったらしい。