AtCoder Grand Contest 024
Updated:
今日は調子が悪かったようで、 A, B, C を通すのにも相当苦労しました。 D をどれだけ考えることができるかというコンテストのようだった。残りの問題はあとで考えてみましょう。
Source codes
Solutions
A - Fairness
$K$ が偶数ならば $A[0] - A[1]$ であり、 $K$ が奇数ならば $A[1] - A[0]$ である。
差を求めるので、 $A[2]$ の存在は関係がない。その影響を取り除くと 2 人の間で $A[0]$ と $A[1]$ を交換しあっているだけになる。だから以上のようにまとめられる。
ポイント
実験してすぐに気づいた。
B - Backfront
$0$-indexed とする。
$i \leq j$ とし、部分列 $i, i+1, \dots, j$ を固定する。 $i-1, \dots, 0$ を順に選び前に移動させる。 $j+1, \dots, N-1$ を順に選び後ろに移動させる。こうすることで昇順に並べ替えることができる。逆にこれ以外の方法では昇順に並べることはできない。したがって、最長の部分列 $i, i+1, \dots, j$ を求めることに帰着する。
これは $P$ の逆置換を $Q$ とすると、 $i \leq j$ であって $Q[i], Q[i+1], \dots, Q[j]$ が増加列となっているものを選ぶことに相当する。つまり $Q[i-1] > Q[i] < Q[i+1] < \dots < Q[j] > Q[j+1]$ のように隣同士を見て不等号を判定するだけでこれはできる。
ポイント
WA を出してしまった。部分列 $i, i+1, \dots, j$ を固定してよいことには気づいていたが、不幸にも $i = 0$ か $j = N-1$ の場合だと思っていた。これはアホだった。 最初と最後だけ見て判定してはならない というやつである。
最長増加部分列だと思っていたが、これは違う。 $Q$ で捉えた時には連続していないといけない。
置換は必ず $0$-indexed で取り扱う ことに注意したい。
C - Sequence Growing Easy
出来上がった数列は必ず下図のグラフのように、傾き $1$ の山形を重ねたものになっている。そしてその総コストはそれぞれの山の高さ $=$ 幅の和である。
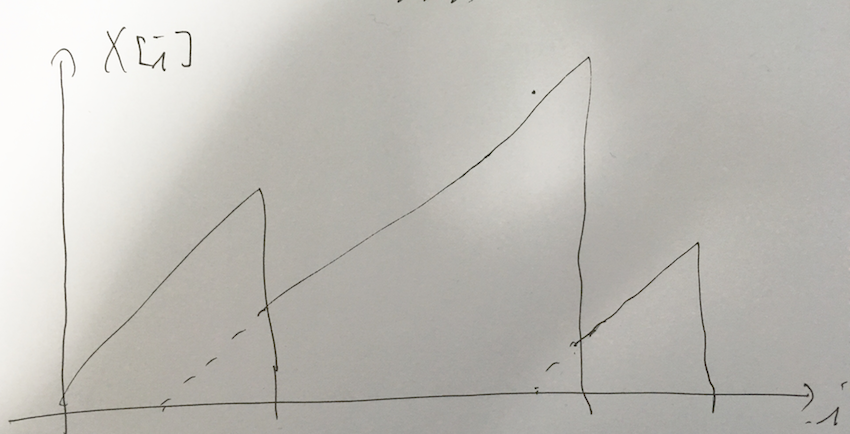
$A$ が構成できる必要十分条件は、 $i = 0, \dots, N-2$ に対し $A[i] + 1 = A[i+1]$ または $A[i] \geq A[i+1]$ が成立することである。そして後者となっている場合に $A[i]$ のコストをその都度払う(ただし $A[N-1]$ は必ず払う)。コストの合計が答えである。
ポイント
長い時間、問題文を間違えて把握していて、何ができるのかを把握できなかった。こういうこともあるか。
D - Isomorphism Freak
コンテスト中に考えられなかったので、あとで自分で考えてから答えを見る。
ポイント
E - Sequence Growing Hard
ポイント
F - Simple Subsequence Problem
ポイント
Others
うまくいかなかったので数学に集中するべき期間のような気がする。来週までに安心してコンテストに臨める環境を整えたい。
