AtCoder Regular Contest 097

AtCoder Regular Contest 097

いやぁ今日はハマってしまいました。正解がわかってから正しく実装するまで結構罠がありました。これをクリアするのは難しかったです。

Source codes

• My submissions (AtCoder)
• My source codes (GitHub)

Solutions

C - K-th Substring

$1 \leq K \leq 5$ なので、答えは最長でも $5$ 文字である。もし $6$ 文字以上の $T$ が答えならば $T[0, 1), T[0, 2), \dots, T[0, 5)$ はそれより辞書順で小さいから不合理である。よって $S$ の $5$ 文字以下の部分列を全て持ってきて $K$ 番目を出力すればよろしい。異なる部分文字列を持ってくるので、 set<string> を用いる。

ポイント

すぐわかった。

D - Equals

Union-Find すればよろしい。用語がないと説明が難しいので、 $i$ 番目に $p_i$ という石が置かれているとする。スワップを繰り返して移動できる先に $i$ という石が置かれているならば、そのスワップを用いて $i$ 番目に $i$ の石をおいてしまえばよろしい。そして移動できる先は、全ての $j$ について $(x_j, y_j)$ を結合した集合の集合のうち $p_i$ が元として属している集合の元全体である。したがって union した後は $i$ と $p_i$ が is_same であるかを尋ねて true ならカウンタを回すだけで良い。

ポイント

Union-Find を早く貼れるかだけである。 ARC 的にはちょっと安直でよくないですね。

E - Sorted and Sorted

最初にネタバレすると、あとで BIT を使いたいので $1$-indexed とする。

遷移を転倒数で書く

ある数字をある場所まで持ってくるために swap する最小回数は、転倒数で決まる。今回の場合、まず

$DP[i][j] = $ 左から $i+j$ 個を見て、白は $1$ から $i$ までソート済み、黒は $1$ から $j$ までソート済みにするまでにかかる最小回数

と定める。答えは $DP[N][N]$ である。初期状態は $DP[0][0] = 0$ である。遷移は、

\[ DP[i][j] = \min(DP[i-1][j] + cost[0][i-1][j], DP[i][j-1] + cost[1][i][j-1]) \]

と求まる。ただし添え字が $0$ 未満になるものは考慮しない。ここで $cost$ が転倒数である。正確に定義すると、

$cost[0][i][j] = $ 初期配置において、白の $i+1$ よりも右側にある「白の $1$ から $i$ までの個数」 $+$ 「黒の $1$ から $j$ までの個数」。

$cost[1][i][j] = $ 初期配置において、黒の $j+1$ よりも右側にある「白の $1$ から $i$ までの個数」 $+$ 「黒の $1$ から $j$ までの個数」。

である。

BIT で転倒数を求める

さて問題はどうやって $cost$ を求めるかということである。これは DP を回す前に BIT を使って高速に求めることができる。黒用の $BIT[0]$ と白用の $BIT[1]$ を用意しておく。左側から見ていき、その数字に出会ったら BIT に入れて、上の数を求める。

具体的には次の通り。今左側から見ていって黒の $i$ に出会ったとする。まず $BIT[0][i] += 1$ とする。次に $j = 0, \dots N$ に対し、

\[ cost[0][i-1][j] = \sum_{k \in [1, i)} BIT[0][k] + \sum_{k \in [1, j+1)} BIT[1][k] \]

とする。白も類比的である。

計算量

$cost$ の前演算は、全部で $2N$ 個あって、数字に出会うたびに $O(\log N)$ で登録して $2N$ 回 $O(\log N)$ で和を問い合わせる。だから計算量は $O(N^2 \log N)$ である。 $DP$ の遷移は $O(N^2)$ である。よって答えは $O(N^2 \log N) + O(N^2) = O(N^2 \log N)$ である。 $N \leq 2000$ なら、オーダーだけ見ると微妙なところだが、 BIT の各ステップは bit 演算と和を取る動作で尽きるため、大変高速で、間に合う。

ポイント

コンテスト中はこちらではなく F に取り組んだわけだが、転倒数はわかっていた。 BIT で転倒数を高速に求めるところだけ、直感的にはわからなかった。これが初見の段階でおぼろげにでも見えていれば取り組んだところではある。以下に掲げた類題に似たような問題があるので復習が足りない。

具体的にいうと、 集合に登録されている「ある数以上の個数」を高速に $N$ 回求めたくなったら BIT を使え である。この日記でも何回か取り上げたことがある。 Binary Indexed Tree を同様の用途で使う類題：

• COLOCON -Colopl programming contest 2018- Final D - Chaos of the Snuke World 考察の後は同じ用途を求められる。偶然にもこれも swap の問題である。
• ARC075 E - Meaningful Mean 条件を convex に書きかえる作業をする。考察の後は 座標圧縮 をすることで結局同じものを数えることができる。

F - Monochrome Cat

自分がコンテスト中に書いた時のメモを添えながら解説をかく。

全ての頂点が B であれば答えは $0$ 秒である。以下ある頂点は W であるとする。

削除して良い点を削除する

まず「末端の B の頂点」を考える。正確に定義すると、 B の頂点であって、そこから生えている辺の数が $1$ であるものである。

この頂点は、削除して考えても良いことがわかる。なぜなら、最初から B であるので色を塗り替える必要はそもそもなく、なおかつその先になんの頂点もない、ゆえに、その頂点にいく必要がないからである。

もちろん、最初にいっぱい頂点が生えていたとしても、削除を続けて最終的に末端の B になってしまったのであれば、もちろんそれは削除することになる。再帰的な操作が必要である。結論から言うと DFS で実装するのが正解なのだが、私が間違えた点であるのであとで議論する。

例えばサンプル 4 でこの操作を行うと、以下の図のようになる。バツをつけたのが削除した点である。

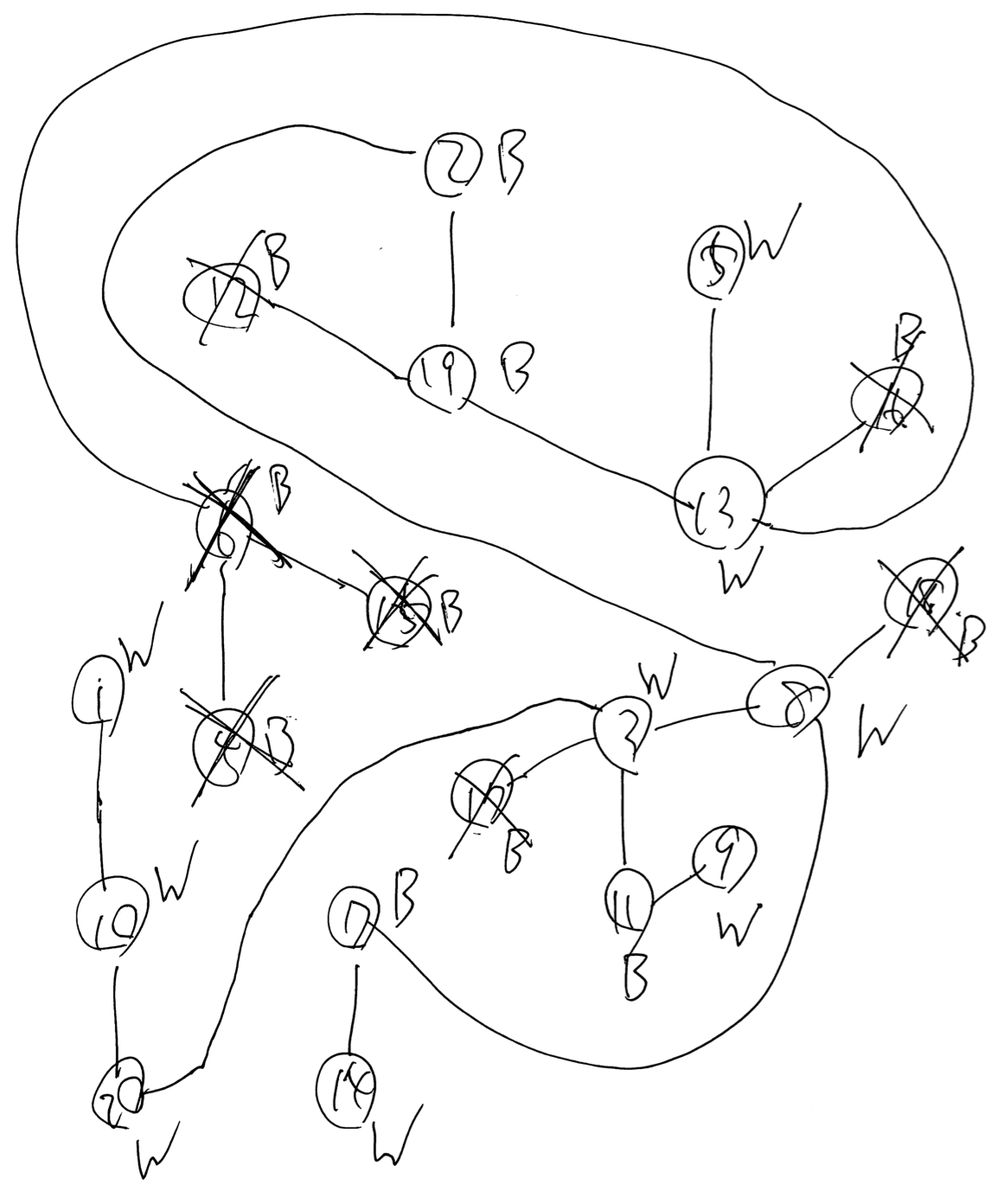
DFS を「くまなく」するのを基準にする

上記の削除した後の木を $T$ とする。頂点の数は $M$ であるとする。

$T$ の「末端の頂点」は必ず W であるから、そこにはたどり着かないといけない。したがって、移動の仕方としては、 適当に root を決めて末端まで DFS して root に戻ってくる しか「ほとんど」ないのである。これを基準にして、できるだけ無駄を減らす方針で解答を考察する。

まず基準となる DFS をした時に、移動に何秒かかるかを測ろう。どれを root でやっても、どれを先に回ろうとも、結果は同じである。というのも、まず移動の回数は辺の数の $2$ 倍、すなわち $2(M-1)$ である。そしてこの結果として、頂点 $e$ にたどり着く回数は $e$ から生えている辺の数である。したがって、

• 生えている辺の個数が偶数でかつ W の頂点
• 生えている辺の個数が奇数でかつ B の頂点

は、色を変えるためにそれぞれ $1$ 秒余計に止まらなければならないことになる。この点にチェックをつけ、この個数を $cost$ とする。例えばサンプル 4 でこの操作を行うと、以下の図のようになる。濃く囲ってチェックマークをつけている点が、 $cost = 3$ を生じさせている点である。

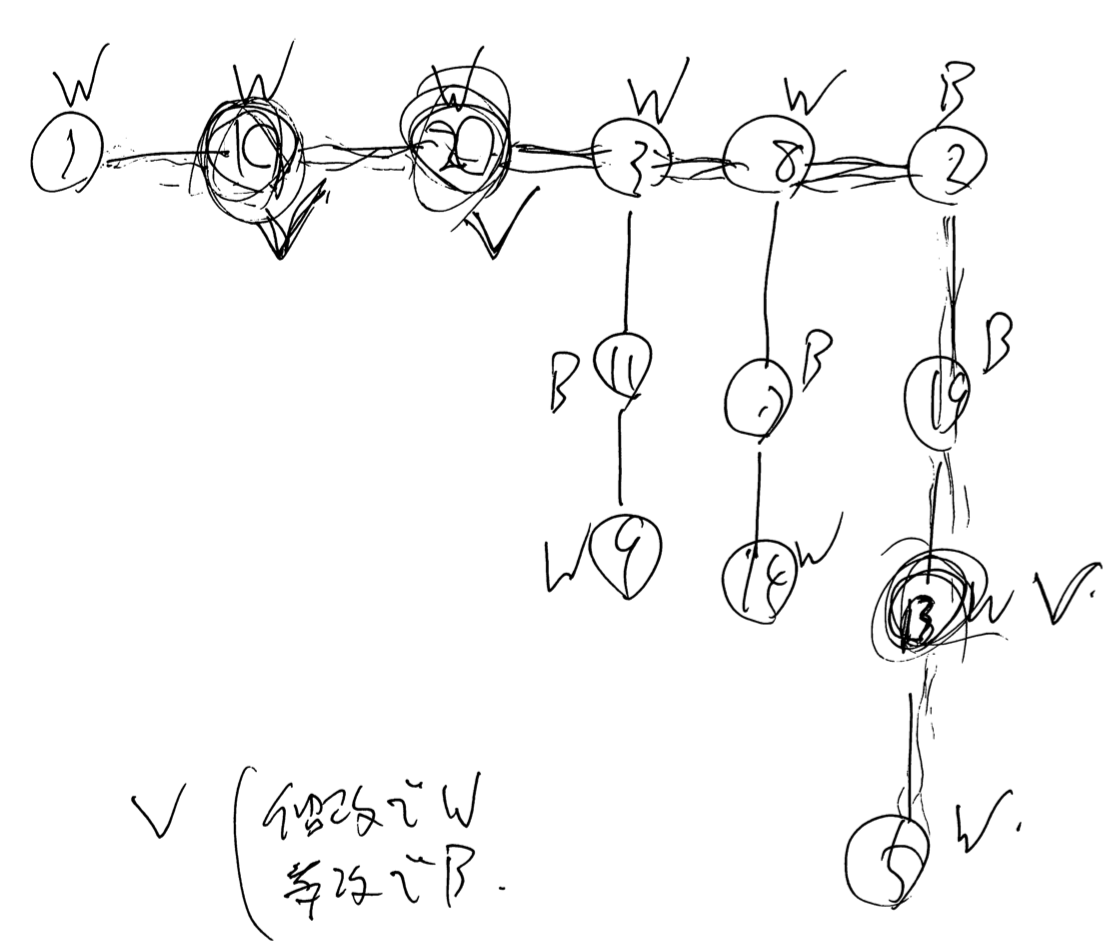
どうすると最善になるか

上で作った経路はループしているので、どこを root とみなしても類比的であるところが強い。この状態から最終結果をさらに小さくするためには、移動する場所を削除するしか方法がない。つまりスタート地点とゴール地点を決めて、先ほどの DFS 経路からゴールからスタートに至る経路を削除するしかない。ただしこの経路の中には末端の W が入ってはならない。

この削除によってどれだけ縮まるか考察すると、次のことがわかる。

命題 1：節約できる総秒数は、削除した経路に含まれるチェックをつけた点の $2$ 倍である。

証明：チェックをつけた点と、チェックがついていない点について、それぞれどうなるのか考察する。点に復路で行かなくなることによって、入ってくる辺の偶数奇数が逆転する。チェックをつけた点に復路で行かなくなることによって、そこに止まる時間がそもそも必要なくなる。したがって $2$ 秒節約できいる。逆にチェックをつけていない点に復路で行かなくなることによって、そこで止まる時間が発生するので、節約は結局できない。よって命題 1 のようにまとめられる。

つまり末端を含まない経路であって、チェックをつけた点を一番多く含むものを求めればよろしい。その点の数を $maxi$ とすると、答えは、 \[ 2(M-1) + cost - 2maxi \] であるとわかる。サンプル 4 の場合 $2 (13 - 1) + 3 - 2 \times 3 = 21$ というわけである。

maxi の求め方

解説によると直径を求めるのと全く同じ方法でよろしいらしい。冷静に考えればそうか。一応下に自分が実際にとった解法を書く。

DFS で求める。まず複雑さを避けるために root は W の点とする。再帰関数 DFS で返却するのは「その頂点を始点とし、子孫方向への末端までまっすぐ走った際の、チェックのついた頂点の最大数」とし、 DFS の中で $maxi$ を更新する ものとする。まず int ans = (S[v] == 'B' ? 1 : 0); として自分を数えておく。次に、子が何人いるかで分類する。

• 子が $0$ 人なら $0$ を返却する。この頂点は必ず W である。
• 子が $1$ 人(それを $e$ とする)なら ans += dfs(e); を $maxi$ の候補として持っておき、 ans を返却する。
• 子が $2$ 人以上いるとすると、 dfs(e) を全部やって、大きい方から順に $X_1, X_2$ とする。
  • $maxi$ の候補は $ans + X_1 + X_2$ である。すなわち、 $v$ を折り目として $X_1, X_2$ 方向を削除した経路が最も節約できる候補である。
  • ans += X_1; として ans を返却する。

以上で解答が可能である。計算量は $O(N)$ である。

ポイント

点が削除できることに気づくまで 30 分程度、次に DFS 経路からどれを削除するとどのくらい減るのかに気づくまで 30 分程度だった。実装時間は 20 分程度しか残ってなかったので、実装ミスがあって、それを直す暇がなくて無理かなと思っていた。実際、得点には至らなかった。

実装で間違えたところは、意外に思うかもしれないが「削除して良い点を削除する」のところである。ここを DFS でやるのが正解だと気づくのがとても遅かった。

次の 2 つの実装は、どちらもナイーブな実装は TLE として弾かれるようにできている。これを正解にすることは可能かもしれないが、単純ではないと思う。

• 末端の B の頂点を queue<int> に入れて BFS する。
• 末端の B の頂点を stack<int> に入れて DFS する。

どうしてこれが不可能であるかというと、同じ頂点を 2 回以上検査する必要があるからである。つまり、末端の頂点をくまなく走査して削除してからでないと初めて削除の判定ができないような点がある。これを安直に bool visited[100010]; などで判定するのは非常に難しい。

木で走査するには DFS が安全 である。どれほど末端から始めたくても、一番遠い root を基準として、末端の処理を再帰関数の中で書くのが安全である。

そもそも今回の条件は再帰的である。 末端から再帰的に定義される条件について、素直に再帰関数の DFS をすればよかったのである。

仮にこれができたとしても実装間に合わなかったので、仕方ないのだが、太字は教訓として持っておきたい。

Others

C - sample: 3, tle: 2.000, time: 06:07, from_submit: 142:26
D - sample: 4, tle: 2.000, time: 08:05, from_submit: 134:22
E - sample: 3, tle: 2.000, time: 00:00
F - sample: 4, tle: 2.000, time: 134:22, from_submit: 00:00