AtCoder Beginner Contest 171
Updated:
Source codes
Solutions
A - alphabet
We use the following if-clause if ('A' <= x && x <= 'Z').
B - Mix Juice
Sort and pick $K$ fruits in ascending order.
C - One Quadrillion and One Dalmatians
Observation
This is not $26$-based numbers. If we write these numbers in $10$-based, we have the followings. \[ 0, 1, 2, 3, \dots, 9, 01, 02, 03, \dots, 09, 10, 11, \dots, 99, 001, 002, \dots \] But for each blocks, it is $26$-based numbers. The $K$-th block gathers $26 ^ K$ numbers whose digit is $K$.
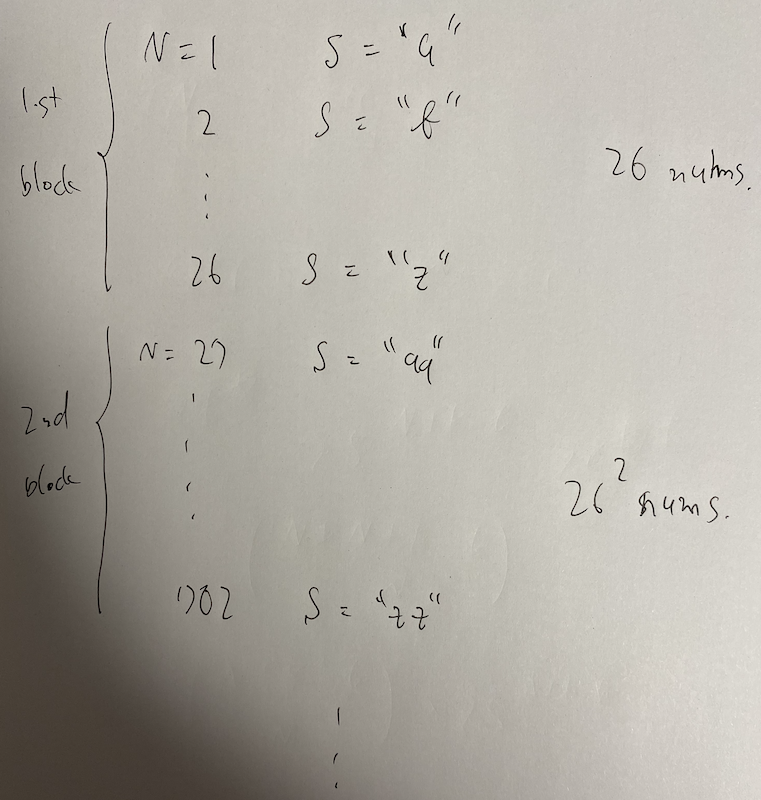
Determine the block
This is just subtract $26, 26 ^ 2, \dots$ from $N$ as long as $N$ is positive.
Determine the string
We convert $N$ into $0$-indexed. Then, we can determine its string by / and % in the normal way.
D - Replacing
Let $H$ be the histogram of $A$ and $S$ be its sum. For each query $(B, C)$, we execute the following.
\[
\begin{align}
H[C] &\mathbin{ {+} {=} } H[B], \\
S &\mathbin{ {+} {=} } (C - B) H[B], \\
H[B] &\gets 0.
\end{align}
\]
E - Red Scarf
Let $x _ i$ be the number that $i$-th person has. Let $X = \oplus _ {i \in N} x _ i$. It holds that \[ a _ i = \bigoplus _ {j \in N \setminus \{ i \} } x _ j = X \oplus x _ i \] Therefore, we have the following relation. \[ \bigoplus _ {i \in N} a _ i = (X \oplus \dots \oplus X) \oplus \bigoplus _ {i \in N} x _ i = 0 \oplus X = X, \] where $(X \oplus \dots \oplus X) = 0$ since $N$ is even. We can calculate $x _ i$ by the following relation. \[ x _ i = X \oplus a _ i. \]
F - Strivore
Observation
We count the number of $T$s of which $S$ is a subsequence. Let $N = \lvert S \rvert$.
Solution #1
$T$ is formed as follows.
\[ T = \overline{S[0]} \dots \overline{S[0]} S[0] \overline{S[1]} \dots \overline{S[1]} S[1] \dots S[N - 1] * \dots * \tag{F.1} \]
Here, $\bar{S[i]}$ means a character except $S[i]$ and $*$ means an arbitrary character.
Let $k$ be the length of $* \dots *$. We will try all $k$s with $0 \leq k \leq K$. The number of this possible frame of (F.1) is \[ \begin{pmatrix} N - 1 + K - k \\ N - 1 \end{pmatrix}. \] For each frame, the number of the string within that frame is \[ (26 - 1) ^ {K - k} 26 ^ {K}. \] Therefore, the answer is \[ \sum _ {k = 0} ^ K \begin{pmatrix} N - 1 + K - k \\ N - 1 \end{pmatrix} (26 - 1) ^ {K - k} 26 ^ {K}. \]
Solution #2
Thinking of the above argument, we come up with the string $S$ itself does not effect the answer, we just use the length $N$. Hence, it suffice to fix $S = aaa \dots aaa$.
Then, the condition for $T$ is that $\lvert T \rvert = N + K$ and that $T$ has more than $N$ ‘a’s. Therefore, the answer is \[ \sum _ {a = N} ^ {N + K} \begin{pmatrix} N + K \\ a \end{pmatrix} (26 - 1) ^ {N + K - a}. \]
