AtCoder Beginner Contest 168
Updated:
Source codes
Solutions
A - (Therefore)
Just use if-clause or array.
B - … (Triple Dots)
Just do as they indicate us to. Use s.substr(0, k);.
C - : (Colon)
We work on the complex plane $\mathbb{C}$. Without loss of generality, we can assume that the 12 o’clock direction is the positive real direction and the two clock hands rotates anti-clockwise.
Let $0$ be the fixed point the problem statement says. Then, the endpoints of the hour hand and that of the minute hand are
\[
\begin{align}
a &= A \exp(2 \pi (h / 12 + m / (60 \cdot 12))), \\
b &= B \exp(2 \pi m / 60).
\end{align}
\]
The answer is $\lvert a - \rvert$.
We can use polar(r, theta);.
D - .. (Double Dots)
Assume $0$-indexed. Execute BFS from $0$ and record each vertex’s parent. Flush them for vertexes $i = 1, \dots, N - 1$.
E - (Bullet)
Solution
Let $v _ i = \begin{pmatrix} A _ i \\ B _ i \end{pmatrix}$. The $i$-th and $j$-th sardines are on bad terms if and only if $(v _ i, v _ j) = 0$, where $(\cdot, \cdot)$ is the normal inner product.
First of all, we count $\sharp \{ i \in N \mid v _ i = 0 \}$. We add it to the answer and hereinafter we assume $v _ i \neq 0$.
We focus on the fact that $v _ i \in \mathbb{Z} ^ 2$. Therefore, we transform each $v _ i$ into its normal form $w _ i$ so that $v _ i \mathbin{//} w _ i$, $\gcd(w _ {ix}, w _ {iy}) = 1$ and $w _ {ix} \geq 0$. Note that $\gcd(0, k) = 0$ for $k \in \mathbb{N}$. We make the histogram of $\{ w _ i \}$ by map<Point, ll> m;.
Let $tmp = 1$. While $m$ is not empty, we take the top $(p, v) \in m$. Let $q$ be the normal form orthogonal to $p$. Let $w = m[p]$. We think of how to choose sardines on good term from these $v + w$ ones and get as follows. \[ tmp \mathbin{\times =} 1 + (2 ^ v - 1) + (2 ^ w - 1). \] After that, we erase $p$ and $q$ from $m$.
Finally, we execute $ans \mathbin{+=} tmp - 1$ and flush $ans$.
F - . (Single Dot)
Solution
We compress $x$-coordinates and $y$-coordinates and think of the resulting grid. The grid is at most $O(N) \times O(M)$. So we can solve this problem by ordinal BFS.
Implement
We use $i _ x$, $j _ x$ to denote the $i$, $j$ indexes of the raw coordinate of $x$, $y$, respectively. We use $x _ i$, $y _ j$ to denote the $x$, $y$ raw coordinate of the index of $i$, $j$, respectively.
Notations
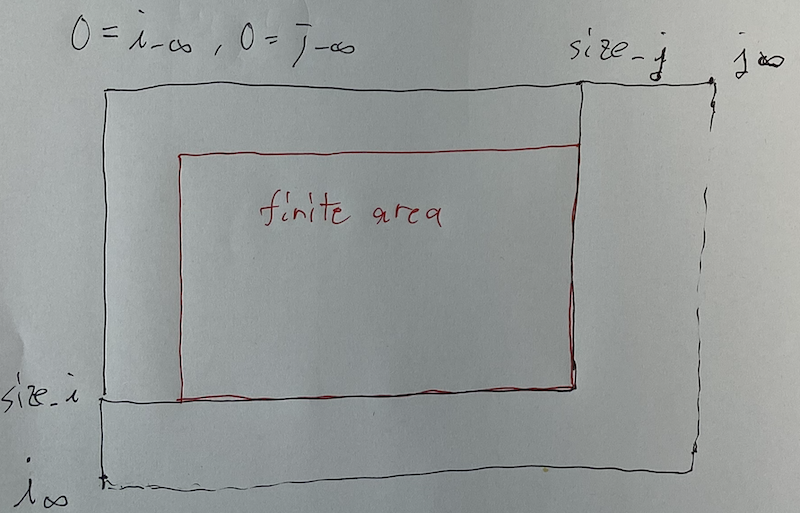
We initialize Compressor<ll> x, y; by $\{ -\infty, 0, \infty \}$. Note that the relation of the point $(i, j)$ and the grid $(i, j)$ is described as the following image.

Considering this, let $size_x$, $size_y$ be (the size of compressors $x$, $y$) $-1$, respectively.
Basics
We see that the actual area of the grid $(i, j)$ is $(x _ {i + 1} - x _ i)(y _ {j + 1} - y _ j)$.
Here, the starting point is $(i _ 0, j _ 0)$. Actually, we need $4$ points, but the constrains says that $(0, 0)$ does not lie on any segments, so just one point suffices.
When is the answer “INF”?
As we argued, we use sentinels $-\infty, \infty$. Therefore, the finite area lies on the grid surrounded by the infinite areas. If we reach the infinite area, the answer is “INF”.
How do we draw a line?
We create the following.
vector<vector<vector<bool>>>$dir[i][j][k] = $ whether we can go in the direction $k$ from $(i, j)$.
We initialize this filling true and by drawing segments we turn some of them into false.
Let $(a, b, c)$ be the north-south line connecting $(a, c)$ and $(b, c)$. Seeing the picture below, we forbid going and coming between $(i, j _ c - 1)$ and $(i, j _ c)$ for $i \in [i _ a, i _ b)$.
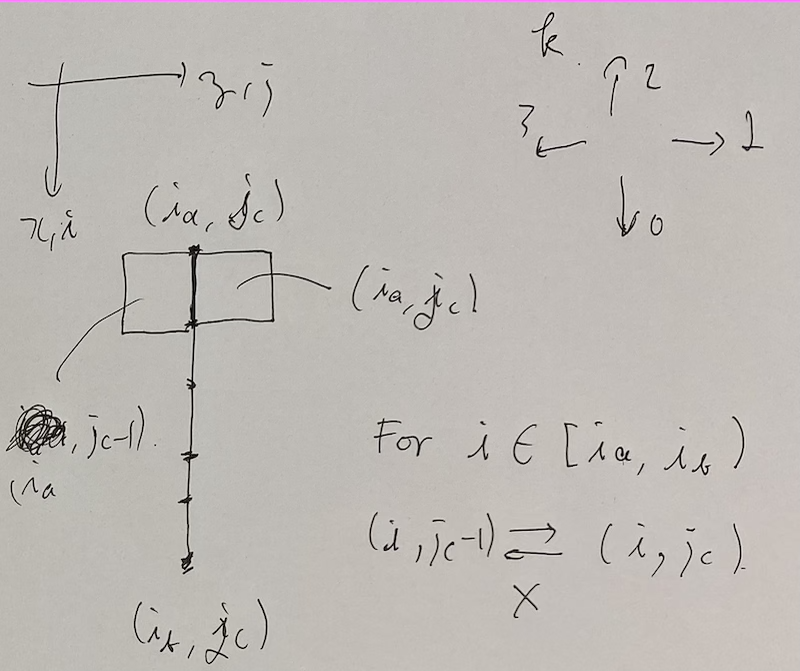
The east-west lines are similar.
We execute BFS to determine the grids where we can reach. We check the answer is “INF” or not. If not, we sum up the actual areas for them and flush the sum.
