Xmas Contest 2019
Updated:
Source codes
Solutions
A - Signboard 1
Very difficult.
B - Set of Integers
C - Sokoban
D - Sum of (-1)^f(n)
E - Sum of f(n)
F - Stamps 1
Observation
We can see that the maximum number of stumps is $4$. The answer is $0$ if and only if there is no empty point on $S$. Hereinafter we assume there is a empty point on $S$.
Given a grid $A$, what’s the condition to color all the points by one stump? It is $h \leq H/2$ and $w \leq W/2$, where $h$, or $w$, is the height, or width, of the minimum rectangle which contains all the empty points within $A$, respectively. This is the necessary and sufficient condition.
Then, what’s the condition to color all the points by two stump? This is not as easy as above, but the two types of sufficient conditions are obvious; $h \leq H / 2$ or $w \leq W / 2$.
We use $f(A)$ to denote the possible minimum number of the stumps to color up all the points of $A$. Let $h$ and $w$ be as above. Let $L$ to denote the rectangle described above.
Hereinafter we can assume that
- $h > H / 2$ and $w > W / 2$, and
- $2 \leq f(A) \leq 4$.
Suppose that $f(A) = 2$. Then, what’s the possibilities of the placement of the two stumps and $L$? This is not so complicated. We can easily find two stumps at least two of whose edges are on the boundary of $L$.
Thus here we reach the point to distinguish $f(A) = 3$ or $4$. Suppose that $f(A) = 3$. Then, what’s the possibilities of the placement of the three stumps and $L$? This is complicated. But we can show the following proposition.
Proposition F.1: Suppose that $f(A) = 3$. Then, there is at least one stump of the three with its at least two edges are shared with the boundary of $L$.
Proof. Suppose to the contrary that any of the three stumps share at most one edge with the boundary of $L$. This immediately contradicts the definition of $L$. We cannot create $L$ by three stumps given this assumption because we lack at least one stump within $L$ to define the four edges of $L$.
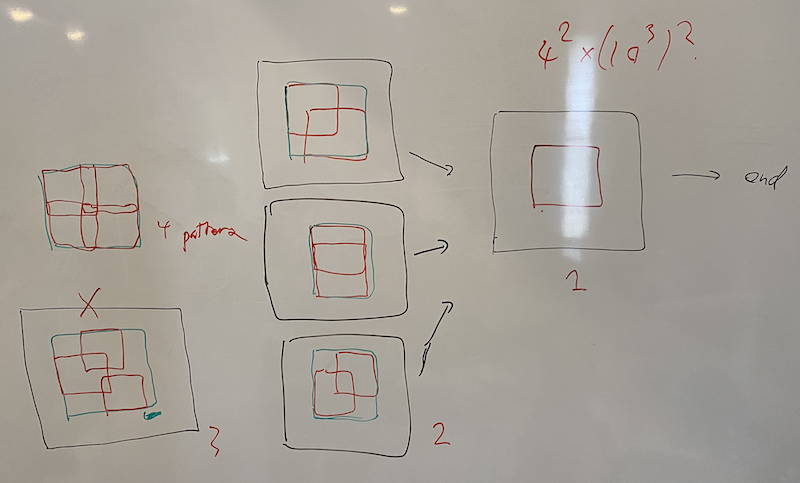
Therefore, to calculate $f(A)$, all we have to do is just execute the DFS for just $4$ possibilities of $L$ for each $A$. If we cannot color up by $3$ stumps by above way, the answer is $4$.
Solution
First we compute $f(S) = 0$ or not. Suppose $f(S) \geq 1$. Then we make the function int dfs(vector<string> const &A, int d);. Here $d$ is the number of the left stumps. We can solve the problem on easy cases and then can assume assert(height > H / 2 && width > W / 2);. Then, we try $4$ possibilities of the stump whose two edges are on the boundary of $L$, just as follows.
int ans{infty};
for (auto k = 0; k < 4; k++)
{
int x{mini_h};
int y{mini_w};
if (k & 1)
{
x = maxi_h - H / 2 + 1;
}
if (k >> 1 & 1)
{
y = maxi_w - W / 2 + 1;
}
vector<string> B(stump(A, x, y));
ch_min(ans, dfs(B, d - 1) + 1);
}
return ans;
The time-complexity is $O(4 ^ 2 HW)$.
G - Stamps 2
We set $P = 5$, $Q = 2$ and $C = P^2 + Q^2$. Note that $P$ and $Q$ are coprime.
Definition G.1: We define the relations $\sim _ A$ and $\sim _ B$ on $\mathbb{Z} ^ 2$ as follows. \[ \begin{align} (x, y) \sim _ A (x’, y’) &\Longleftrightarrow (\exists a, b \in \mathbb{Z})(x - x’ = Pa + Qb \land y - y’ = -Qa + Pb), \tag{G.1} \\
(x, y) \sim _ B (x’, y’) &\Longleftrightarrow (\exists a, b \in \mathbb{Z})(x - x’ = Qa + Pb \land y - y’ = -Pa + Qb). \end{align} \]
It is elementary to see both $\sim _ A$ and $\sim _ B$ are equivalence relations.
Observation
First of all, let’s work on the following lemma.
Lemma G.2: For $(x, y) \in \mathbb{Z} ^ 2$, we have the following. \[ \begin{align} (x, y) \sim _ A (x + C, y), \tag{G.2} \\
(x, y) \sim _ B (x + C, y), \\
(x, y) \sim _ A (x, y + C), \\
(x, y) \sim _ B (x + C, y), \\
\end{align} \]
Proof. To see (G.2), we set $a = P$ and $b = Q$. The others follow almost in the same way.
By Lemma G.2, without loss of generality, when we find an empty point $(x, y) \in S$, we can regard all the points $(x + kC, y + k’C) \in \mathbb{Z} ^ 2$ as empty. Thus we can solve the same problem on $G = (\mathbb{Z} / C \mathbb{Z}) ^ 2$. When we write $(x, y) \in G$, we will mean that $0 \leq x, y < C$.
Definition G.3: Let $(x, y) \in G$ and $0 \leq k < C$. We say $(x, y)$ is level $k$ on $A$, or $B$, if $(x, y) \sim _ A (k, 0)$, or $(x, y) \sim _ B (k, 0)$, holds, respectively.
The next lemma is important.
Lemma G.4: For any $(x, y) \in G$, there exist exactly one pair of numbers $(k _ A, k _ B)$ with $0 \leq k _ A, k _ B < C$ so that $(x, y)$ is level $k _ A$ on $A$ and level $k _ B$ on $B$.
Proof. The arguments on the $A$-side and the $B$-side are completely the same. Thus we forget the letter $A$ or $B$.
First, we show the existence of $k$. Although this is done by direct calculus, here we give an elementary proof. Let $a = 0$. Then since $Q$ (or $P$) and $C$ are coprime, there exist $k$ so that $(x, y) \sim (k, 0)$ by some Euclid method.
Second, we show the uniqueness of $k$. Suppose that there exist $k$ and $k’$ with $0 \leq k, k’ < C$ so that $(x, y)$ is both level $k$ and $k’$. Thus we have $(k, 0) \sim (k’, 0)$. Therefore we have $0 = -Qa + Pb$; here we work on $A$, but on $B$ the same. Since $P$ and $Q$ are coprime, there exists $l \in \mathbb{Z}$ so that $a = Pl$ and $b = Ql$. Then, we have $k’ - k = Pa + Qb = P ^ 2 l + Q ^ 2 l = C l$. Since $0 \leq k, k’ < C$, we admit $k = k’$ with $l = 0$; otherwise either $k$ or $k’$ is out-of-range. This completes the proof.
Solution
Let $p = (x, y) \in T$ be an empty point. By Lemma G.4, there exist exactly one pair of numbers $(k _ A, k _ B)$ with $0 \leq k _ A, k _ B < C$ so that $p$ is level $k _ A$ on $A$ and level $k _ B$ on $B$. We regard $p$ as an edge $(k _ A, k _ B + C)$. We construct a graph consisting of these edges.
What we want to calculate the size of its minimum point cover. Since the uniqueness of the levels, this graph is bipartite. Therefore, the answer is the size of the maximum matching of this graph.
The number of the vertexes $V$ is $2C$ and the number of the edges $E$ is less than or equal to $C^2$. We can compute the maximum matching in $O(\lvert V \rvert \lvert E \rvert) = O(C ^ 3)$-time. Therefore the time-complexity is $O(C^3)$.
Basic knowledge
Definition G.5: Let $G = (V, E)$ be a graph.
- A set of the edges $M \subset E$ is a matching if edges on $M$ has no common vertex as their end points.
- A set of the edges $F \subset E$ is an edge cover if for any $v \in V$ there exists $e \in F$ so that $e = (v, * )$ or $( *, v)$.
- A set of the vertexes $S \subset V$ is a stable set if for any $v, w \in S$ it holds that $(v, w) \not \in E$ and $(w, v) \not \in E$.
- A set of the vertexes $S \subset V$ is a point cover if for any $e = (u, v) \in E$ it holds that either $u \in S$ or $v \in S$.
Proposition G.6: Let $G = (V, E)$ be a graph.
- If $G$ has no isolated point, it follows that \[ \lvert \text{maximum matching} \rvert + \lvert \text{minimum edge cover} \rvert = \lvert V \rvert. \]
- It follows that \[ \lvert \text{maximum stable set} \rvert + \lvert \text{minimum point cover} \rvert = \lvert V \rvert. \]
- If $G$ is a bipartite, it follows that \[ \lvert \text{maximum matching} \rvert = \lvert \text{minimum point cover} \rvert. \]
