DISCO Presents Discovery Channel Code Contest 2020 Qual
Updated:
DISCO presents ディスカバリーチャンネル コードコンテスト2020 予選
Source codes
Solutions
A - DDCC Finals
Solve it as it indicates us to.
B - Iron Bar Cutting
We can try all of the notches. If the original bar is split into $A$ and $B$, we have to pay at least $\lvert A - B \rvert$ and it is enough since we just adjust the shorter one to reach the longer one. Here, $A$ and $B$ are calculated by accumulated sum in $O(1)$ for each $N$ cases. The time complexity is $O(N)$.
C - Strawberry Cakes
Easy cases
Suppose that all lines has at least one strawberry. Then, first we cut the all lines. Now the problem is $1$-dimensional. It can be solved by some greedy algorithm since each cake’s size is not necessarily the same. It is sure that the cut cakes consist of rectangles.
General cases
In case that some lines has no strawberry, first we ignore them and solve the problem for each line containing strawberries as above. Then, we can expand those lines to the empty lines by just copying them. It is suffice to work iteratively on two adjacent lines which the one side is done and the other is empty. Just copying the former to latter is suffice. They keep generating rectangles.
D - Digit Sum Replace
Observation
First, we focus on one pair $(x, y)$. When it is merged, it will become
- one element $x + y$ if $x + y \leq 9$;
- two elements $(1, x + y - 10)$ if $x + y \geq 10$,
since $0 \leq x + y \leq 18$.
Next, we see the manipulates above from the viewpoint of the general cases. We use $N$ to denote the number of elements and $S$ to denote the sum of them. Then, the former is regarded as a manipulation $(N, S) \mapsto (N - 1, S)$ and the latter $(N, S) \mapsto (N, S - 9)$.
Solution
Therefore, it is useful for us to consider $T = 9N + S$. Then, every manipulation reduces $T$ by $9$ at any time in any case. At the initial state $T _ 0 = T$ is fixed of course. The state is terminated at some fixed number $1 \leq K \leq 9$ whatever manipulations are done. $K$ is computed by $S \% 9$. Note that if it is $0$, we have $K = 9$ instead of $0$. Thus at the final state $T _ 1 = T$ is fixed. Therefore the number of manipulations is $X = (T _ 0 - T _ 1) / 9$. It does not depend on any details of manipulations. The answer is $X$.
My dirty solution during the contest
We go back on one pair $(x, y)$. To merge those two elements, we spend one or two operation(s). In general cases, it is also true. We use manipulations at least $N - 1$ times. We want to spend as many manipulation as possible. How many times can we spend more? The upper bound is $S / 10$ since what we want is the manipulation $(x, y) \mapsto (1, x + y - 10)$ and it occurs at most $S / 10$ times.
This upper bound is reachable as follows. We try from right to left. If we have $(x, y) \mapsto x + y$, we use it again. If we have $(x, y) \mapsto (1, x + y - 10)$, we left $1$ and we use $x + y - 10$ for the next manipulation. Then, the state will be $1, 1, 1, 1, \dots, 1, x$ after $N - 1$ manipulations. Here $1$ appears $S / 10$ times. Then merging them takes at least $S / 10$ manipulations. We have reached the upper bound.
This can be done recursive ways to arrive at the terminal state. Since we have kept the upper bound, it gives the answer.
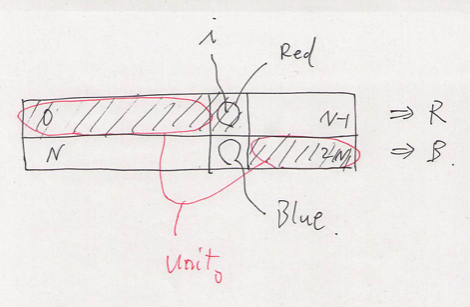
E - Majority of Balls
Suppose $0$-indexed. We say an array whose size is $N$ is red or blue if its majority is red or blue respectively.
Solution
First we ask $A _ N = [0, \dots, N - 1]$. Without loss of generality, we can suppose $A _ N$ is red. We define
\[
A _ i = [0, \dots, i - 1] + [N + i, \dots, 2N - 1].
\]
Then, $A _ 0$ must be blue. Therefore, by binary search, we can find $0 \leq i \leq N - 1$ so that $A _ i$ is blue and $A _ {i + 1}$ is red. Then, we have the node $i$ is red, $N + i$ is blue and both of the following $(N - 1)$-sized arrays have the same number of red and blue balls.
\[
\begin{align}
unit _ 0 &= [0, \dots, i - 1] + [N + i + 1, \dots, 2N - 1], \\
unit _ 1 &= [N, \dots, N + i - 1] + [i + 1, \dots, N - 1]
\end{align}
\]
So for each $j \in unit _ 1$, we ask whether $unit _ 0 + [j]$ is red or blue. It is definitely the color of $j$. We can determine the color of the elements in $unit _ 1$, and $unit _ 2$ too.
F - DISCOSMOS
We use H, R, D to denote a robot of type-H, R, D, respectively.
Case $T = 1$
First, we solve the problem when $T = 1$. There are three patterns.
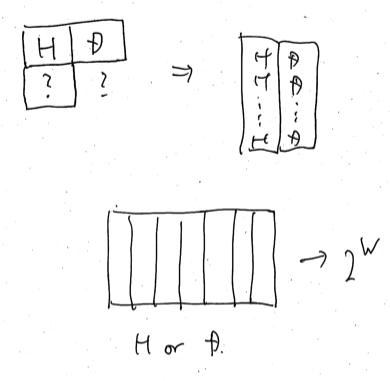
H and D
Suppose we have the pair of adjacent robots H and D. Then, what can come under the H? If it is R, it will hit with D in a second. If it is D, it will hit with H after some seconds since here the grid is a $2$-dimensional torus. Therefore we must have H under the H. Then, what can come under the D? If it is H, the rule breaks in a second. If it is R, the rule breaks in some seconds. So it must be D.
Therefore, we have the pair of adjacent two columns of H and D. We see the whole of the grid. If we have a R, it hits the column consisting of H in some seconds. Therefore, we conclude that there is no R. To be short, the whole grid is composed of the $W$ columns that consist of exactly either H or D. The number of the valid grid of this pattern is $2 ^ W$.
H and R
Suppose we have the pair of adjacent robots H and R. The argument and the conclusion is almost the same. There is no W and the whole grid is composed of the $H$ lines that consist of exactly either H or R. The number of the valid grid of this pattern is $2 ^ H$.
No H
We consider the grid where there is no H. How can we put R and D? It is difficult.
First, we consider the necessary condition. We focus on a diagonal line. If we put a R and a D on the same diagonal line, they hit each other in some seconds. Therefore on the same diagonal line we put exactly one-type robots of either H or D. And this is sufficient since whether we put H or D does not effect the fact that in a second all robots on that line go to the next line.
The number of the diagonal line on this torus-gird is $G = \mathrm{gcd}(H, W)$. The number of the valid grid of this pattern is $2 ^ G$.

Eliminating double count
We eliminate the double counting problems. The first and second case both includes the grid that consists of all H. We have to subtract $1$ from. The third case includes the grid that consists of all D or R, which we have already counted in the first or second cases. We have to subtract $2$ from them.
General $T$
We have solved the problem when $T = 1$. We use $solve(H, W)$ to denote its answer and $solve(H, W, T)$ to denote the general case’s. When $T$ is general, it is not so different from the case $T = 1$. Let $G _ H = \mathrm{gcd}(T, H)$ and $G _ W = \mathrm{gcd}(T, W)$. In case $T = 1$, we worked on a simple gird, but it is a graph. In general cases, in terms of graphs, it will be split into $G _ H G _ W$ distinct grid-graphs whose height is $H / G _ H$ and whose width is $W / G _ W$. Therefore we have \[ solve(H, W, T) = solve(H / G _ H, W / G _ W) ^ {G _ H G _ W}, \] which completes the solution.
Others
I am qualified! See you in January 2020.
