NIKKEI Programming Contest 2019-2
Updated:
Source codes
Solutions
A - Sum of Two Integers
Just flush $(N - 1) / 2$.
B - Counting of Trees
Solution
First we check if $D[0] = 0$ and $D[i] > 0$ for $i > 0$; otherwise the answer is $0$. We set
$A[j] = \sharp \{ i \in N \mid D[i] = j \}$.
We can forget the given integers of the vertexes. Just counting is enough. The answer is \[ \prod _ {i = 0} ^ {N - 1} A[i]^{A[i + 1]}. \]
C - Swaps
Observation
We argue on $0$-indexed.
First, we forget the maximum number of the manipulations. Without loss of generality, we can assume $B _ 0 \leq B _ 1 \leq \dots \leq B _ {N - 1}$. The best strategy for $\{ A _ i \}$ is that we sort $\{ A _ i \}$ by the ascending order. This sorting takes at most $N - 1$ manipulations. We state this as the following theorem.
Theorem B.1: Let $p \in \mathfrak{S} _ N$. Let $G _ p = (V, E)$ be a graph with $V = N$ and $E = \{ (i, p _ i) \mid i \in N \}$. Then, the number of swaps we need to generate $p$ is $N - C$, where $C$ is the number of the connected components of $G$.
Proof: First of all, we check the connected components of $G$ are cycles. We don’t need to swap the vertexes which are not on the same connected components. Thus we will work on one fixed connected component $K$ of $G$. First, we show that we need at least $\sharp K - 1$ swaps to make the component $K$. If $\sharp K = 1$, there is nothing to show. Thus suppose $\sharp K \geq 2$. When we swap $i, j \in K$, we color $e = (i, j)$. If we make less than $K - 1$ swaps, the colored edges won’t make a spanning tree, which means there is at least one vertex which has not been touched yet. This is impossible. Second, we show that we can make $K$ by $\sharp K - 1$ swaps. This is very straightforward. Just taking $\sharp K - 1$ edges on the cycles. Summing up these results, we can make $G$ by $\sharp G - C \times 1 = N - C$ swaps and this is the best result.
Let $A’$ be the sorted version of $A$. If there exists $k \in N$ so that $A’[k] > B[k]$, the answer is No immediately. Hereinafter we assume that $A’[i] \leq B[i]$ for $i \in N$. Let $p \in \mathfrak{S} _ N$ so that $p _ {A[i]} = A’[i]$. By Theorem B.1, if $G _ p$ is not one whole cycle, we can gain $A \mapsto A’$ by less than $N - 1$ swaps. The answer is Yes.
How to reduce the number of manipulations
Hereinafter, we assume that $G _ p$ is a whole simple cycle. The sorting $A \mapsto A’$ needs $N - 1$ swaps. We have to give up $A \mapsto A’$. Then, how can we reduce the number of manipulations?
We think of a sufficient condition.
Lemma B.2: Assume that $G _ p$ is a whole simple cycle. Then, if there exists $k \in N$ so that $A’ _ {k + 1} \leq B _ k$, the answer is
Yes.
Proof: We set $q \in \mathfrak{S} _ N$ as follows.
\[
q _ i = \begin{cases}
p _ {k + 1} & i = k, \\
p _ k & i = k + 1, \\
p _ i & \text{otherwise}.
\end{cases}
\]
We consider $G _ q$. Since $G _ p$ is a whole simple cycle, $G _ q$ consists of two “split” cycles divided by $k$ and $k + 1$. This can be made by $N - 2$ swaps and it satisfies the condition since $A’ _ {k + 1} \leq B _ k$. We conclude that the answer is Yes.
And this is the necessary condition, too.
Lemma B.3: Assume that $G _ p$ is a whole simple cycle. Then, if $A’ _ {i + 1} > B _ i$ for all $i \in (N - 1)$, the answer is
No.
Proof: We show that we have to use $A’ _ i$ for $B _ i$ to hold $A _ i \leq B _ i$ for each $i \in N$ by mathematical induction on $i$. For $i = 0, 1, \dots, N$, we consider which element of $\{ A’ _ i \}$ should be used for $B _ i$. Since $B _ i < A’ _ {i + 1} \leq A’ _ {i + 2} < \dots$, we have to use one element of $A’ _ 0, A’ _ 1, \dots, A’ _ i$. But the assumption of induction, we have already used $A’ _ 0, \dots, A’ _ {i - 1}$, which forces us to use $A’ _ i$ for $B _ i$. This means that, to hold $A _ i \leq B _ i$ for each $i \in N$ we must sort $A \mapsto A’$, which need $N - 1$ swaps. Therefore the answer is No.
D - Shortest Path on a Line
Solution
Let $G = (N, E)$ be the original graph. Let $G’ = (N, E’)$ be a graph so that $E$ consists of the following edges; we use $(u, v, c) \in E’$ to denote the edge whose source is $u$ and whose destination is $v$ and whose cost is $c$.
- $(i + 1, i, 0)$ for each $i \in (N - 1)$.
- $(L _ j, R _ j, C _ j)$ for each $j \in M$.
We show the following proposition later.
Proposition C.1: The minimum costs of the paths from $0$ to $N - 1$ on $G$ and $G’$ are the same.
Thus the solution is just to use the Dijkstra method on $G’$.
Proof of Proposition C.1
Proof: Let $A$ and $A’$ be that minimum cost on $G$ and $G’$, respectively. First we show that $A \geq A’$. This is easy. We fix a minimum path $P$ from $0$ to $N - 1$. We can make a path $P’$ that attains the total cost being $A$ on $G’$. Just using $(L _ j, R _ j, C _ j)$ and returning back by $(i + 1, i, 0)$ are suffice.
Second we show that $A = A’$. The edges of $E’ \setminus E$ are $(i + 1, i, 0)$ for each $i \in (N - 1)$. Let $d _ i$ be the distance between $0$ and $i$. We show that $\{ d _ i \}$ is a non-decreasing sequence to complete the proof. Let $0 \leq i < j < N$. We fix a minimum path $p _ j$ from $0$ to $j$. There are several steps. But the condition we are given in the problem statement guarantee that we can stop and change the final step smaller to reach $i$ by the cost less than or equal to $p _ j$. This means that $p _ j \leq p _ i$. This is what we want to show.
E - Non-triangular Triplets
Observation
We omit “$K + \dots$” part to write the numbers.
Consider one of the tuples $(A, B, C)$. To hold that $A + B \leq C$, The bigger $C$ is, the better. In addition the less $A$ and $B$ are, the better. Thus we use $2N, \dots, 3N - 1$ for $C$. Thus we work on how to assign $0, \dots, 2N - 1$ for $A + B$ side. Once we’ve assigned by the best strategy, we can check if the answer is proper or not easily.
What is the best strategy?
We will use $\{ 0, 1, \dots, 2N - 1 \}$ for $A$ and $B$. The sum is $N (2N - 1)$. We want to the best assignment, that means $A + B$ should be an arithmetic progression whose difference is $1$. We use $X$ to denote its start number. Thus the best strategy should be as follows: $A _ 0 + B _ 0 \leq X$, $A _ 1 + B _ 1 \leq X + 1$, $\dots$, $A _ {N - 1} + B _ {N - 1} \leq X + N - 1$. The sum of the right hand side is $XN + N(N - 1)/2$. Thus we have the lower bound of $X$ as follows. \[ XN + \frac{N (N - 1)}{2} \geq N (2N - 1), \ \ \ \text{ i.e. } \ \ \ X \geq \frac{3N - 1}{2}. \]
$X$ is an integer. We should divide the solution into two cases; $N$ is odd and $N$ is even.
First, we consider the case $N$ is odd, that is, $N = 2M + 1$. Then we have $X \geq 3M + 1$. We search for the assignment that satisfies this equation. We can find the solution as follows.
\[
\begin{align}
0 &+ && 3M+1 &= && 3M+1 = X, \\
M+1 &+ && 2M+1 &= && 3M+2 = X+1, \\
1 &+ && 3M+2 &= && 3M+3 = X+2, \\
M+2 &+ && 2M+2 &= && 3M+4 = X+3, \\
2 &+ && 3M+3 &= && 3M+5 = X+4, \\
\dots &+ && \dots &= && \dots, \\
M-1 &+ && 2M+N-1 &= && 3M+N-2 = X+N-3, \\
2M &+ && M+N-1 &= && 3M+M-1 = X+N-2, \\
M &+ && 2M+N &= && 3M+N = X+N-1. \\
\end{align}
\]
Second, we consider the case $N$ is even, that is, $N = 2M$. Then we have $X \geq 3M - 1/2$. Actually, we can find the best solution as follows.
\[
\begin{align}
0 &+ && 3M &= && 3M \leq X, \\
M &+ && 2M &= && 3M \leq X+1, \\
1 &+ && 3M+1 &= && 3M+2 \leq X+2, \\
M+1 &+ && 2M+1 &= && 3M+2 \leq X+3, \\
\dots &+ && \dots &= && \dots, \\
M-1 &+ && 3M+M-1 &= && 3M+N-2 \leq X+N-2, \\
2M-1 &+ && 2M+M-1 &= && 3M+N-2 \leq X+N-1. \\
\end{align}
\]
F - Mirror Frame
Observation
First, we assign the unique number for each line. Observe what lines are assigned for a point $(i, j)$. We can see that exactly the two lines whose number are $x = \lvert i - j \rvert$ and $y = \min(i + j, 2N - i - j)$ are assigned for $(i, j)$.
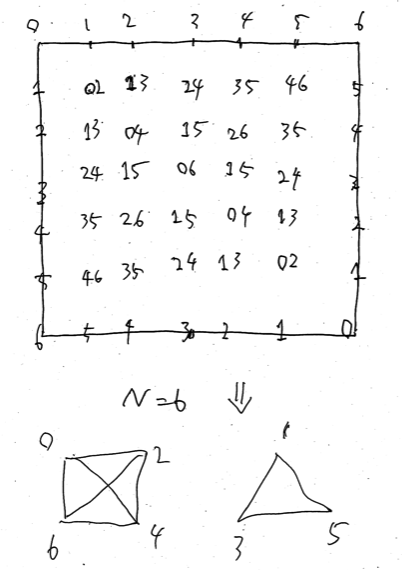
We convert a point $(i, j)$ in this plane into an edge $(x, y)$ on the graph $G$. What is the graph $G$? $G$ is a pair of the perfect graphs. We convert the problem into another problem described as follows.
Constraints: We are given two perfect graphs. Each edge on the graph $G = (X, E)$ is assigned on$=1$, off $=0$ or
?.
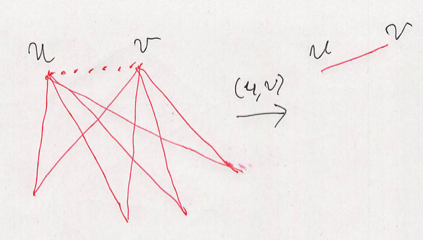
Manipulation: Choose two vertexes $u, v$. We change on/off for all edges which contains either $u$ or $v$.
Aim: By several manipulations, we want to make all edges be off.
Answer: The number of assignments on all?for on/off so that we achieve the aim.
Lemmas
Here we will solve a flipping problem. So we prepare $\mathbb{F} _ 2$-vector space. For all $e _ \lambda \in E$, we use $a _ \lambda \in \mathbb{F} _ 2$ to denote its state, i.e.,
\[
a _ \lambda = \begin{cases} 0 & e _ \lambda \text{ is off}, \\
1 & e _ \lambda \text{ is on}. \end{cases}
\]
Let $V$ be a vector space on $\mathbb{F} _ 2$ as follows.
\[
V = \left\{ \sum _ {e _ \lambda \in E} a _ \lambda e _ \lambda \mid a _\lambda \in \mathbb{F} _ 2 \right\},
\]
where $\sum$ is a formatting sum, equipped with the normal $+$ and the normal scalar $\cdot$.
We focus on the subspace $W \subset V$ generated by the manipulations.
Lemma F.1: Let $u, v, w \in X$. Then the triangle $uvw$ is included in $W$, i.e., \[ (u, v) + (v, w) + (w, u) \in W. \tag{F.1} \]
Proof: We do three manipulations on ($u$ and $v$), ($v$ and $w$) and ($w$ and $u$). Let $e \in E$. Then, $e$ is chosen $0$ times if neither of vertexes of $e$ is $u$, $v$ or $w$, $2$ times if exactly one of vertexes of $e$ is $u$, $v$ or $w$, and $3$ times if $e = (u, v)$, $(v, w)$ or $(w, u)$. Thus we have (F.1).
Lemma F.2: Suppose $\lvert X \rvert$ is even. Then, we have $W = V$.
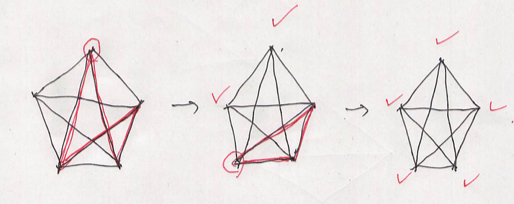
Proof: If $\lvert X \rvert \leq 2$, we have nothing to show. Suppose $\lvert X \rvert \geq 4$. Let $e _ 0 = (u, v) \in E$. For all $w \in E \setminus \{ u, v \}$, we apply Lemma F.1 for the triangles $uvw$. Note that in this process, $(u, v)$ is chosen a even-number times ($= \lvert X \rvert - 2$ times). Then, we manipulate on $u$ and $v$ to have $e \in W$. Then it follows that $W = V$ since $W$ is a linear subspace.
Lemma F.3: Suppose $\lvert X \rvert$ is odd. Then, $W$ consists of all sub-graphs of $G$ where the in-out-degree of any vertex is even.
Proof: The manipulation changes the in-out-degree of any vertex by even number. So, if there is a vertex whose in-out-degree is odd, it won’t be included in $W$. On the contrary, let $g$ be a sub-graph of $G$ where the in-out-degree of any vertex is even. We check all vertexes in some fixed order. We visit $v _ k$ after we visit $v _ 0, \dots, v _ k$ whose in-out-degree is $0$. By our assumption, the in-out-degree of $v _ k$ is always even. We divide them into some pairs and make triangles by Lemma F.1. Then, the in-out-degree of $v _ k$ is zero. We can work iteratively to make all in-out-degrees be $0$. This means $g \in W$.
Solution
The final answer is the multiplication of the answers of two graphs.
By Lemma F.2, if $\lvert X \rvert$ is even, we can choose on/off for each ? arbitrarily.
If $\lvert X \rvert$ is even, things are complicated. We think of the forest of ?-edges on $G$. We work on each connected component $C$ of the forest. First, we count the number of $1$-edges between $C$ and $G \setminus C$. If it is odd, the answer is $0$. We cannot achieve our goal in this case since all manipulations changes the in-out-degrees of all vertex by even number.
If it is even, however, we can create solution by the same argument in Lemma F.3. How many possibilities are there? We take a spanning tree $T$ on $C$. We can choose on/off for each edges of $C \setminus T$ arbitrarily and then work on $T$. The statements of $T$ is determined iteratively by its leaves. Thus the possibility is $2 ^ {\lvert C \setminus T \rvert}$.
