AtCoder Grand Contest 039
Updated:
Source codes
Solutions
A - Connection and Disconnection
Basic Strategy
Suppose we have a function $f(S)$ that flushes the correct answer. Then, we can basically see that the answer is described as the following form: $f(KS) = A(K - 1) + B$, where $A, B$ is a constant.
This is seen through the construction of $f$. We write $N = \lvert S \rvert$. For $i = 1, \dots, N - 1$, if $S[i - 1] = S[i]$, we change $S[i]$ for some character that must be different from $S[i + 1]$, such as #. This greedy method works well if there exists $j$ so that $S[j - 1] \neq S[j]$. We divide $S$ into $T + U$ and we have
\[
f(KS) = f(T) + f((K - 1) (U + T) ) + f(U) = f(T) + f(U) + (K - 1) f(U + T).
\]
So we set $B = f(T) + f(U) = f(S)$ and $A = f(U + T)$.
To write the code, it is easy for us to compute $B = f(S)$ and $A + B = f(2S)$.
Corner Cases
If the string is composed only by one character, the strategy above doesn’t work. We can see this problem by the single character S = "a". We have $f(a) = 0$, $f(aa) = 1$, $f(aaa) = 1$, $f(aaaa) = 2$, $f(aaaaa) = 2$, and so on.
In this case the answer is $NK/2$.
B - Graph Partition
When can we construct the solution?
First, let us show the following lemma.
Lemma B.1: We can construct the solution if and only if the graph is a bipartite graph.
Proof. Suppose we have constructed the solution $\{ V _ i \}$. We color each $e \in V _ i$ red if $i$ is odd and blue if $i$ is even. Then, the constraints confirm that each edge must connect a red vertex and a blue vertex. That means the graph is bipartite. Suppose the graph is a bipartite graph. Then, we can easily construct $V _ 0$ which contains all red vertexes and $V _ 1$ which contains all blue vertexes.
So we have to decide if the graph is a bipartite graph or not. If not, the answer is -1.
The answer
We show the next lemma.
Lemma B.2: Suppose the graph is a bipartite graph. Then, the answer is the diameter $+1$.
Proof. Let $D$ be the diameter. By Lemma B.1, we can construct $\{ V _ i \}$. Assume to the contrary that the answer is greater than $D + 1$. Then, we can take a path whose length is greater than or equal to the answer by the graph’s connectedness. This contradicts the definition of the diameter. Thus the answer must be less than or equal to $D + 1$. In addition, we can construct $V _ 0, \dots, V _ D$ as follows. We take a pass $v _ 0, \dots, v _ D$ that attain the diameter. We set $V _ i$ as follows.
$V _ i = $ the set of the vertexes whose distance with $v _ 0$ is $i$.
Obviously, $v _ i \in V _ i$, especially $v _ D \in V _ D$. For any edge $e = (u, v)$, the difference of the distance between $u$ and $v _ 0$ and the distance between $v$ and $v _ 0$ is less than or equal to $1$. If it were $0$, it would break the bipartite property. Thus the difference is $1$, which satisfies the constraints.
How to compute the diameter
It is well-known that how to compute the diameter of a tree. We just do DFS twice and the time complexity is $O(N)$. But this problem, the graph is not necessarily a tree. We can compute, however, its diameter by definition: \[ D = \max _ {u, v} d(u, v). \] We use the Warshall-Floyd algorithm to calculate $d(u, v)$ for all $u$ and $v$ in $O(N^3)$-time.
C - Division by Two with Something
Examine some samples
The manipulation is described in binary as follows.
- $[…]0$ -> $1[…]$,
- $[…]1$ -> $0[…]$.
Thus every binary whose size is $N$ returns its initial state by $2N$ times. But we want to know the minimum number of manipulations. The period seems to be critical. Let’s see two cases.
- $1010$ -> $1101$ -> $0110$ -> $1011$ -> $0101$ (the conjugation of the initial state) -> -> -> -> $1010$. We have taken $8$ times now.
- $111000111$ -> $011100011$ -> $001110001$ -> $000111000$ (the conjugation of the initial state) -> -> -> $111000111$. We have taken $6$ times this time.
Therefore, we see the following.
Proposition C.1: Let $T = S \bar{S} S \bar{S} S \dots S$ be a binary whose length is $N$. Then, $T$ returns by manipulating $2 \lvert S \rvert$ times.
Solution
For $K = 1, \dots, N$, we check $N \% K = 0$ and $K$ is odd. If so, let $L = N/K$ and $S$ be the prefix of $X$ whose length is $L$.
First, we consider $S$ as a binary number. Then, for $S’ = 0, \dots, S - 1$, we consider $T = S’ \bar{S’} S’ \dots S’$ by repeating $S$ and $S’$ for $K$ times. It follows that $T < X$, both as strings and as binaries. Thus we have obtained $c = S$ binaries which needs $2K$ times manipulations.
Second, we consider $T = S \bar{S} S \dots S$. If $T \leq X$, we have another good binary, so the count will be added by $c \mathbin{ {+} {=} } 1$; otherwise nothing more is needed.
We hold the results $(L, c)$ above as map<int, mint>. There are “double-count problems” here. We can solve this by very easy way. For example, we count $S = 010101$ as $6$ period, it must have been counted as $2$, and every $2$-period $S$ have been counted as $4, 6, 8, 10, \dots$. So in the ascending order of $L$, we subtract that number the counts for $2K, 3K, 4K, \dots$. This is the same way as the sieve of Eratosthenes. We have eliminated “double-count problems”.
The answer is \[ \sum _ {(L, c) \in map} 2Lc. \] The time complexity is $O(PN + N \log \log N)$, where $P$ is the number of the $K$ so that $N \% K = 0$ and $K$ is odd. Since $N \leq 2 \times 10^5$, $P$ is very small. Actually it holds that $P \leq 72$.
D - Incenters
Terms
| 日本語 | English |
|---|---|
| 内心 | incenter |
| 重心 | centroid |
| 外心 | circumcenter |
| 垂心 | orthocenter |
| 傍心 | excenter |
| 二等分線 | bisection |
Solution
Let $O = (0, 0)$ be the central point of the unit circle $K$. On $K$, we take three different points $A, B, C$. Let $I$ be the incenter of $\triangle ABC$. Let $A’$ be the central point of the arc $BC$ without $A$. We define $B’, C’$ as the similar way. Then, we see that $I$ is the orthocenter of $\triangle A’B’C’$. Note that $O$ is the circumcenter of $\triangle A’B’C’$, too. Let $G$ be the centroid of $\triangle A’B’C’$. Here, we use the Euler line, i.e. $3\vec{OG} = \vec{OI}$. Therefore, we conclude that \[ \vec{OI} = 3\vec{OG} = \vec{OA’} + \vec{OB’} + \vec{OC’}. \tag{C.1} \]
We fix $B$ and $C$. Then $A’$ is also fixed, provided that the relative positions of $A, B, C$ are the same. We count how many points are on the two arcs $BC$ respectively and add them up to $A’$. This solution works in $O(N^2)$-time.
E - Pairing Points
Suppose $0$-indexed.
Basic strategy
We can solve this problem by a recursive method. First, let’s see what happens when we connect $0$ and $i$. Since the $N$ edges makes a huge tree, we have some sub-trees derived from $(0, i)$. We use the term “unit” to denote each of them. We forget the detailed structure of them. We can say that each unit consists of some range of $[1, i - 1]$ and $[i + 1, 2N - 1]$ and its range follows correctly.
To make the situation simple, we work on the straight line between $0$ and $2 N - 1$. We can describe the units the following picture.
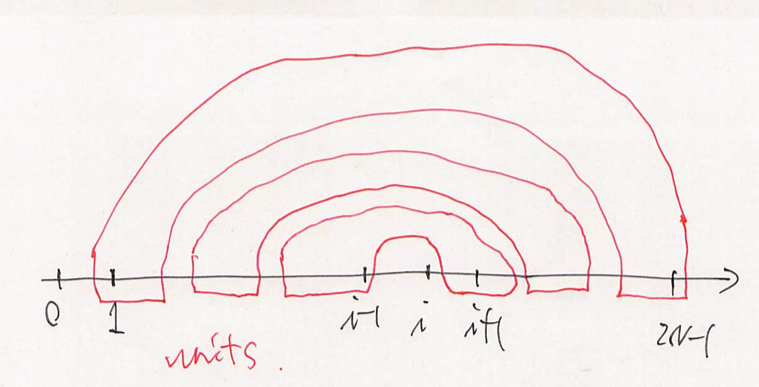
Convert into memo-recursion
We use the boolean function $connect(i, j)$ which is true if we are allowed to connect $i$ and $j$; otherwise false.
Definition
$calc(A, B, C, D) = $ the number of one or some units consisting of the range $[A, B]$ and $[C, D]$,
$calc\_unit(A, B, C, D) = $ the number of exactly one unit made by the range $[A, B]$ and $[C, D]$,
Here, $0 \leq A \leq B < C \leq D \leq 2N - 1$.
Answer
To avoid the double-counting problem, first we work on the edge $(0, i)$. Then, we write the answer $X$ in the following way.
\[
X =
\begin{cases}
\displaystyle \sum _ {i = 2} ^ {2N - 2} calc(0, i - 1, i + 1, 2N - 1) & N \geq 2, \\
1 & N = 1 \land connect(0, 1), \\
0 & N = 1 \land \lnot connect(0, 1).
\end{cases}
\]
Transition
Basic ideas are simple. We calc $calc\_unit(A, B, C, D)$ by summing up the result in case splitting $i \in (A , B)$ and $j \in (C, D)$ if $connect(i, j)$. We calc $calc(A, B, C, D)$ by separating the one inner unit.
First, we argue on $calc\_unit$. In general cases, this is straightforward as we argued just before.
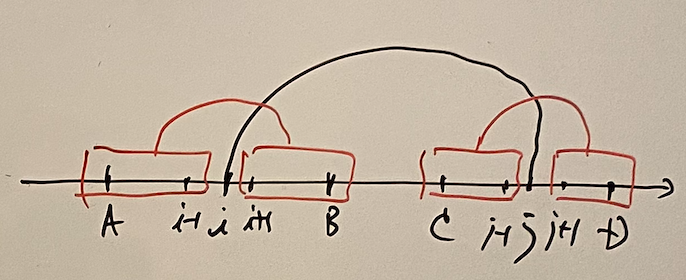
\[ calc\_unit(A, B, C, D) = \sum _ {(i, j) \in S} calc(A, i - 1, i + 1, B) calc(C, j - 1, j + 1, D), \tag{E.1} \] where \[ S = \{ (i, j) \mid A + 1 \leq i \leq B - 1 \land C + 1 \leq j \leq D - 1 \land connect(i, j) \}. \]
Note that $i$ runs on $(A, B)$ and $j$ runs on $(C, D)$ since, if we were to leave one side non-empty and the other side empty, it would cause the halt.
Second, we argue on $calc$. In general cases, we separate it into two cases.
- One inner unit + one or some outer units (non-empty).
- Just one inner unit.
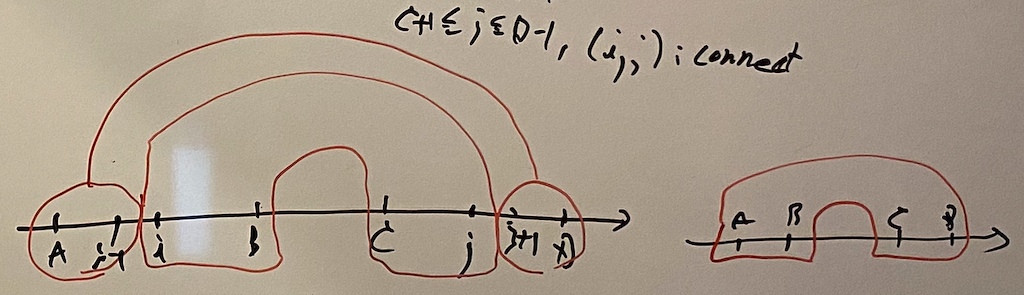
\[
\begin{align}
calc(A, B, C, D) =& \sum _ {A + 1 \leq i \leq B, C \leq j \leq D - 1} calc(A, i - 1, j + 1, D) calc\_unit(i, B, C, j) \\
&+ calc\_unit(A, B, C, D).
\end{align} \tag{E.2}
\]
“Initial state”
The most difficult point of this problem is that how we “stop” the recursion, i.e., to set up the correct “initial states” by exclude some special cases from the above general transitions.
We argue on the “edge” cases. We focus on the case $A = B$ on $calc\_unit$. In this case, we connect $A$ and $j \in (C, D)$ and make units only on the right side. Thus it follows that \[ calc\_unit(A, A, C, D) = \sum _ {C + 1 \leq j \leq D - 1, connect(A, j)} calc(C, j - 1, j + 1, D). \]
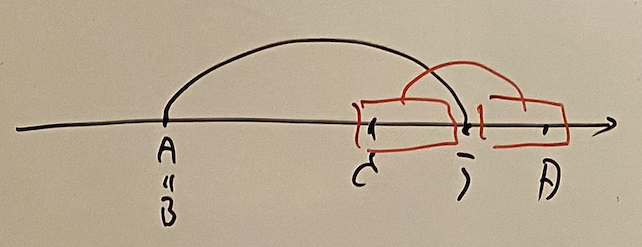
The case $C = D$ is almost the same. \[ calc\_unit(A, B, C, C) = \sum _ {A + 1 \leq i \leq B - 1, connect(i, C)} calc(A, i - 1, i + 1, B). \]
In addition, we don’t forget the case $A = B \land C = D$. \[ calc\_unit(A, B, C, C) = \begin{cases} 1 & connect(A, C), \\\ 0 & \lnot connect(A, C). \end{cases} \]
This is not completed yet. The two $calc\_unit$ pass their calculation to $calc$ but we don’t stop $calc$ yet. But it is not complicated. If we have either $A = B$ or $C = D$, it must be made by one unit. Therefore, we have \[ calc(A, B, C, D) = calc\_unit(A, B, C, D) \text{ if } A = B \lor C = D. \]
Time complexity
The number of the states is $O(N^4)$. Each states calculated by $O(N^2)$-time. Therefore its time-complexity will be $O(N^6)$. We have $N \leq 20$ and $2N \leq 40$. Is it really OK?
Actually, it can be completed in the time limit. We can forget the calculation of “initial state” since it is completed in $O(N)$ or $O(1)$-time. In (E.1) and (E.2), $i$ runs on $(A, B)$ and $j$ runs on $(C, D)$. So we have $A < i < B < C < j < D$. Therefore we can divide the number of states by $6!$, i.e., the number of total functional calls will be around \[ \frac{(2N)^6}{6!} \approx 5.67 \times 10^6, \] which can be completed in the time limit.
In addition, we can calculate the most difficult case by our hand. It is $N = 20$ and all of the nodes are connectable. Then, the answer is $16332922290300$ and the total function calls of $calc$ and $calc\_unit$ occurs $10595863$ times.
