AtCoder Beginner Contest 128
Updated:
- Review: 2020-05-17
- Review: 2020-07-05
Source codes
Solutions
A - Apple Pie
$(3A + P)/2$ を出力する。
B - Guidebook
私の解答
ary << [s, -q, i] として ary.sort.each{|s, q, i| puts i } とする。
ポイント
解説放送の snuke さんから
string s;
int p;
int id;
tie(s, p, id) = a[i];
cout << id << endl;
とする方法を学んだ。また
V.push_back(tie(s, p, i));
は
V.emplace_back(s, p, i);
として良いらしい。
C - Switches
解説放送の解答
bit で全探索するのだが、少し頭を使うと実装が簡単になる。
$V[i] = i$ 番目のスイッチを押した時に $j$ 番目の電球の状態が変わるなら $j$ 番目の bit が $1$ であり、そうでないなら $0$ であるような $2$ 進数、
$res = j$ 番目の電球が最終状態で点灯していて欲しいなら $1$ 、そうでないなら $0$ であるような $2$ 進数。
とする。すると 求めるものは xor をするだけで判定できる 。 \[ \sharp \left\{ S \subset N \mid \bigoplus _ {i \in S} V[i] = res \right\} \] である。これを実装すると楽である。
for (auto i = 0; i < M; i++)
{
int k;
cin >> k;
for (auto j = 0; j < k; j++)
{
int s;
cin >> s;
s--;
V[s] |= 1 << i;
}
}
for (auto i = 0; i < M; i++)
{
int p;
cin >> p;
res |= p << i;
}
ポイント
いやはや xor に気づけば非常に実装が簡単だっただけに、単純作業そうな問題に見えてももっと頭を使おうと自分に言いたい。
ちなみに $N, M \leq 300$ くらいでも解ける。 $\mathbb{Z} / 2 \mathbb{Z}$ で吐き出し法を使う。解空間の次元を $n$ とすると答えは $2^n$ である。
D - equeue
解説放送の解答
左から $l$ 個、右から $r$ 個出すのを全探索する。とりあえずこれらを出す。 そして可能なら負の数を消し去る操作をする。 $0 \leq l, r \leq K$, $l + r \leq N, K$ が条件である。消すことができる回数は $d = K - l - r$ 回である。
ポイント
先に出すものを決めうちするのが大事である。
E - Roadwork
解説放送の解答
斜めだからわかりづらい。問題を言い換える。
時刻 $[L _ i - X _ i, R _ i - X _ i)$ に座標 $X _ i$ に壁が置かれる。時刻 $D _ j$ に正の方向に半直線を伸ばす。壁がぶつかるのはどの座標か。ぶつからない場合は $-1$ を出力せよ。
そこで以下を定める。 typedef tuple<ll, int, ll> event; とする。ここで真ん中の変数は、 $0$ なら壁を置く、 $1$ なら壁を取り除く、 $2$ なら半直線発射とする。最初のが時刻、最後のが壁が置かれる座標である。 vector<event> V; とする。
$0$-indexed とする。 $i = 0, \dots, N - 1$ に対し、 $V \gets (S _ i - X _ i, 0, X _ i)$, $V \gets (T _ i - X _ i, 1, X _ i)$ とし、 $i = 0, \dots, Q - 1$ に対し、 $V \gets (D _ i, 2, 0)$ とする。これらを sort し処理をする。壁の座標を multiset<ll> M; で持っておけばよろしい。 $0$ の操作がきたら $M \gets X _ i$ とし、 $1$ の操作がきたら $M \to X _ i$ とする。その上で $2$ の操作がきたら $M$ の最小値を出力すれば良い。 $M = \emptyset$ の場合はもちろん $-1$ を出力する。 $\{ D _ i \}$ は昇順なので即出力して十分である。
Another solution
Suppose that people go through the all walls. The person $i$ hits the wall $j$ if and only if \[ S _ j \leq X _ j + D _ i < T _ j. \] This is equivalent to that \[ S _ j - X _ j \leq D _ i < T _ j - X _ j. \] Here, $i$ and $j$ are independent of each other. We apply scheduling method for this problem. The rest is the same.
ポイント
これはすぬけさんと同じ解法だった。ただもっと綺麗に書くことができた。早く書ける方針を思いつけば F で得点ができたので、要練習。
F - Frog Jump
解説放送の解答
$C = A - B$ とする。 $C \geq 1$ でないといけないのはすぐわかる。するとジャンプは \[ 0, A, C, C + A, 2C, 2C + A, \dots, xC + A = N - 1 \] の順番になる。ここで $C, x$ が決まれば $A = N - 1 - xC$ は決まる。 $C \geq 1$ を決めた後 $x = 0, 1, 2, \dots$ とすることを考える。すると score が徐々に変わっていくことがわかる。具体的には $score \mathbin{ {+} {=} } s[xC]$, $score \mathbin{ {+} {=} } s[N - 1 - xC]$ とする。ここで $ans \gets max(ans, score)$ とやり続ければ良いが、どこで終わるかがポイントとなる。以下の点に注意する必要がある。
- 座標が $[0, N)$ からはみ出してはいけない。 $xC \geq N$ ならば break する。
- 同じ座標を通ってはいけない。これは
set<int> S;を宣言して insert していけばいい。 $N - 1 - xC \in S$ ならば break, そうでなければ insert, $xC \in S$ ならば break, そうでなければ insert とする。 - $B > 0$ でなければならない。 $1$ 歩数目から $2$ 歩目で前側にジャンプしてはいけない。 $A = N - 1 - xC$ であり、 $B = A - C$ であるから、 $B \leq 0$ ならば break する。
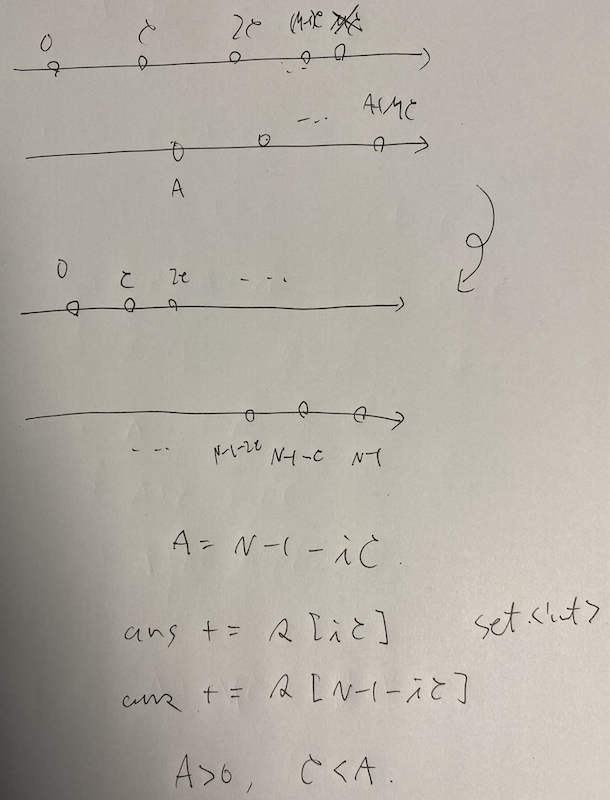
計算量は、 $O(N^2)$ のように見えるが、 $C = 1, \dots, N - 1$ に対して $x \leq (N - 1) / C$ しか探索されないので十分間に合う。 set に問い合わせる計算量も考えると計算量は $O(N (\log N)^2)$ となる。
ポイント
3 の条件を忘れていて時間内に解答できなかった。
Others
A - sample: 3, tle: 2.000, time: 02:02, from_submit: 109:33
B - sample: 2, tle: 2.000, time: 02:42, from_submit: 106:51
C - sample: 3, tle: 2.000, time: 05:24, from_submit: 101:27
D - sample: 3, tle: 2.000, time: 15:36, from_submit: 85:51
E - sample: 1, tle: 2.000, time: 43:41, from_submit: 42:09
F - sample: 3, tle: 2.000, time: 42:10, from_submit: 00:00
反省点の多いコンテストだった。実装量の多い方針を取っているところをもう少し減らして F に充てれば全完できていた。
