AtCoder Regular Contest 060
Updated:
- Review: 2020-07-05
Source codes
Solutions
C - 高橋君とカード / Tak and Cards
Assume $0$-indexed.
Solution
The condition that the average of $y _1, \dots, y _m$ is $A$ is equivalent to that the average of $y _ 1 - A, \dots, y _m - A$ is $0$, i.e., its sum is $0$. Therefore, we execute $x _ i \mathbin{- =} A$ first.
DP part
Let $C = 10000$.
Definition
vector<vector<ll>>$dp[i][j] =$ the number of ways to choose elements from $x[0, i)$ with its sum being $j$.
Initial state
$dp[0][C] = 1$. Otherwise $0$.
Answer
$dp[N][C] - 1$, since we have to exclude the empty set.
Transition
For $i = 0, \dots, N - 1$, for $j = 0, \dots, 2C - 1$, we execute the followings.
\[
\begin{align}
dp[i + 1][j] &\mathbin{+=} dp[i][j], \
dp[i + 1][j + x _ i] &\mathbin{+=} dp[i][j] & (0 \leq j + x _ i < 2C).
\end{align}
\]
D - 桁和 / Digit Sum
This problem is about sqrt-decomposition. Let $m = 10 ^ 6$.
Solution
First, we think of easy cases. If $s > n$, it is impossible, so the answer is -1. If $s = n$, the answer is $n + 1$. Hereinafter, we assume that $s < n$.
For $2 \leq b < m$, we try honestly. For $b > m$, we use another method. Let $p = n / b$ and $q = n \% b$. Then, it follows that $n = pb + q$. Since $b ^ 2 > n$, we have $p < b$. Thus the recursion of $f$ stops and it follows that $s = p + q$. Therefore, we have $n - s = p(b - 1)$. Note that $n - s > 0$. If $p = 0$, it implies that $n = q = s$. Thus, hereinafter we consider of the case $p \geq 1$. Then, $b - 1$ is a divisor of $n - s$. We can try them all.
The time complexity is $O(m) = O(\sqrt{n})$.
E - 高橋君とホテル / Tak and Hotels
This is a doubling problem. Let $M = 30$ be such that $2 ^ M > 10 ^ 5$.
Solution
We prepare for the queries in $O(NM)$-time and answer for each query in $O(M)$-time.
We define as follows.
$v[i][j] = $ the largest id of the hotels we can visit in $2 ^ i$ days from $j$-th hotel.
We fill $v[0][j]$. This is done by two-pointers method. Then, we apply doubling method for $v[i][j]$ such as $v[i][j] \gets v[i - 1][v[i - 1][j]]$.
For each query $(a, b)$, we can assume $a < b$ without loss of generality. We try $i = 29, \dots, 0$ so that we can move $a \gets v[i][a]$ as close to $b$ as possible, not reaching or overcoming $b$. The answer is its cost $+1$.
Point
Let $r(i) = v[0][i]$. This problem is to calculate $\min \{ n \in \mathbb{N} \mid r ^ n(a) \geq b \}$. We want to apply binary search for $n$. In this case, we use doubling method.
F - 最良表現 / Best Representation
Let $n = \lvert w \rvert$.
Solution
If the string consists of only one type of characters, the answer is $n$ and $1$.
The following proposition is a key to solve this problem.
Proposition F.1: If $w$ does not consist of only one type of characters, the minimum number of the terms of the best representation is $1$ or $2$.
We prove this proposition later. We consider how to solve this problem given this proposition.
How to judge given string is good or not #1 (Suffix Array)
We create a function bool is_good(int a, int s); where we determine whether $w[a, a + s)$ is good or not. We test if $w[a, a + s)$ has a period $d$ or not for all the possibilities of $d$ which can divide $s$ with $d \neq s$. This means that the LCP of $w[a, n)$ and $w[a + d, n)$ is greater than or equal to $s - d$. We can do this check by suffix array.
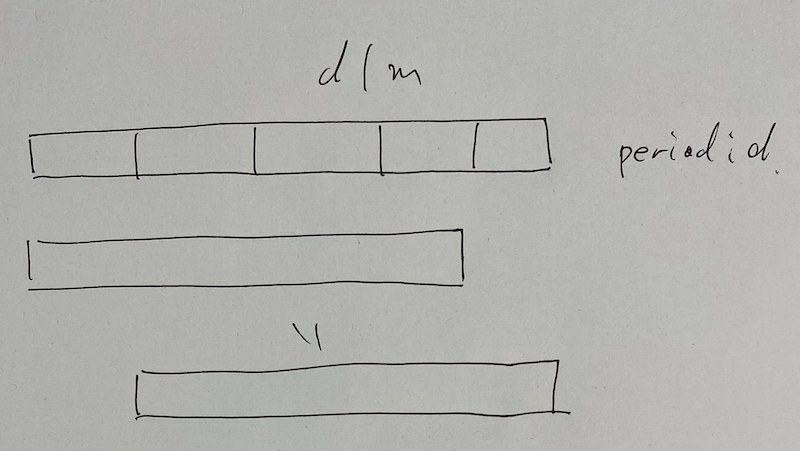
We can gather all the divisors on $[1, n]$ in $O(n \log n)$-time. This is similar to sieve of Eratosthenes. For the case the answer is $1$, we check is_good(0, n). For the case the answer is $2$, we try all $i = 1, \dots, n - 1$ to see is_good(0, i) && is_good(i, n - i). Count the numbers and flush it.
How to judge given string is good or not #2 (KMP algorithm)
We can also use KMP algorithm. With MP-array of a string $S$, we can calculate $S[0, i)$’s period.
int period(int i) const
{ // The period of S[0, i).
auto tmp{i - A[i]};
if (i % tmp == 0)
{
return tmp;
}
return i;
}
This is because $i$-th element of MP-array means that the longest common length of prefixes of $S$ and suffixes of $S[0, i)$. But be careful for the mid-terms. For instance, consider the case $S = $”abcabcab”. Then, its mp arrays says that $8$ th element of MP-array is $5$, but its period is not $3$. Therefore, we need to check about divisors.
We make MP-array for $w$ and reversed $w$. Then, the idea is the same above.
Proof of Proposition F.1
It suffice to show that either of $w$ or $w[0, n - 1)$ is a good string. Suppose to the contrary that both of them are non-good string. Let $p$ and $q$ be the period of $w$ and $w[0, n - 1)$, respectively. Since $p$ divides $n$, $q$ divides $n - 1$ and $\gcd(n, n - 1) = 1$, it follows that $\gcd(p, q) = 1$. Note that $p \geq (n - 1) / 2$ and $q \geq n / 2$.
Let $0 \leq a < b < n$. We will show that $S[a] = S[b]$. There exists such $k, l \in \mathbb{N}$ that $\lvert b - a \rvert = kp - lq$. For any $i \in n$, at least either $i - q \geq 0$ or $i + p < n$ follows since the length of the string $S$ is greater than or equal to $p + q$. In addition, it also follows that $S[i - q] = S[i] = S[i + p]$, where the indexes are not out-of-range. Therefore, it follows that $S[b] = S[a + kp - lq] = S[a]$ if we show that there is a path between $a$ and $b$.
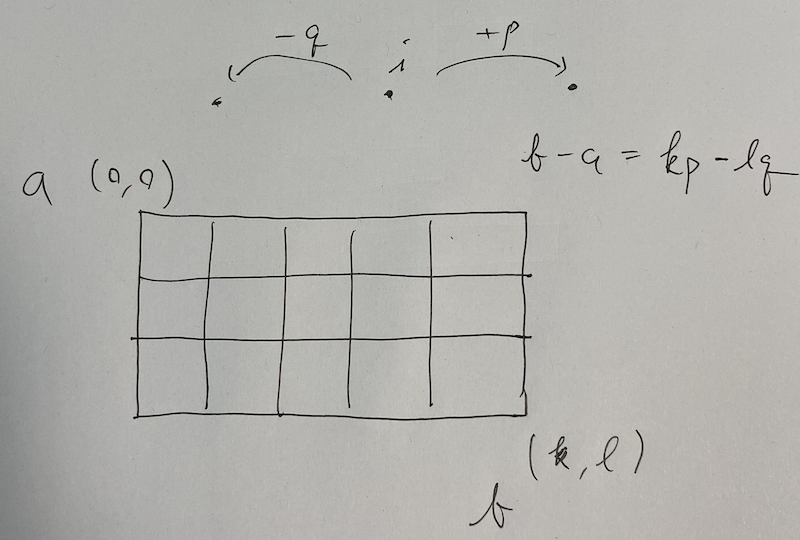
There are two type of possibilities of stalemates. Suppose that there exists $l’ < l$ that we come to $a + kp - l’q$ but cannot transit $a + kp - l’q \to a + kp - (l’ + 1)q$. This means either $a + kp - (l’ + 1)q < 0$ or $a + kp - (l’ + 1)q \geq n$. If the former held, we would have $b < 0$. If the latter held, we would have $a + kp - l’q \geq n$. Both of them are contradictions. Suppose that there exists $k’ < k$ that we come to $a + k’p - lq$ but cannot transit $a + k’p - lq \to a + (k’ + 1)p - lq$. This is also impossible proved in the same way. This completes the proof.
References
- AtCoder ARC 060 F - 最良表現 (900 点) (けんちょんの競プロ精進記録) by drken-san
- Especially, how to judge … #2.
