Tokio Marine & Nichido Fire Insurance Programming Contest 2020
Updated:
Source codes
Solutions
A - Nickname
Flush S.substr(0, 3).
B - Tag
If $V \leq W$, the answer is NO.
Suppose that $V > W$. Let $D = \lvert A - B \rvert$ and $U = \lvert V - W \rvert$. If $UT \geq D$, the answer is YES; otherwise, NO.
C - Lamps
Honest implementation takes $O(N)$-time for each manipulation by cumulated sum.
We see that we can stop when $A _ i = N$ holds for all $i$. The worst case appears $N = 2 \times 10 ^ 5$ and $A _ i = 0$ in the initial state. But it takes just $41$ times.
D - Knapsack Queries on a tree
Assume $1$-indexed for vertexes.
Solution
We construct the following DP table for each vertex $v \leq 2 ^ C$ where $C = 9$ since $2 ^ C \approx \sqrt{N}$.
$dp[v][i] = $ the largest value where the total weight of the items is less than or equal to $i$.
We construct this table in $O(\sqrt{N} L)$-time, where $L \approx 10 ^ 5$.
For each query $(v, l)$, we divide the items we are considering into two blocks. Let $w$ be the largest ancestor of $v$ which satisfies $w \leq 2 ^ C$. In fact, $w$ may or may not be $v$ itself. Let $S = \{ (v _ k, l _ k) \}$ be the set of the items we have not considered to create $dp[v]$. We apply brute-force method for $S$ to try all the possibilities of the subset of $S$ and ask the remaining weight to $dp[v]$ to obtain the maximum value.
Each query takes $O(\sqrt{N})$-time. Therefore, the total time complexities is $O(\sqrt{N} L + \sqrt{N} Q)$.
E - O(rand)
Observation
Reduction
At first, we work on each bit. Note that $S$ is bitwise-and and $T$ is bitwise-or.
- If $S = 0$ and $T = 1$, the answer is $0$.
- If $S = T = 1$, we delete such $A _ i$ that its bit is $0$.
- If $S = T = 0$, we delete such $A _ i$ that its bit is $1$.
Therefore, we can reduce the problem so that $S = 1$ and $T = 0$ and the bit runs on $[0, M)$. We rescale $A$ and $N$.
Inclusive-exclusive principle
The problem becomes as follows.
Problem E.1: Find the number of ways to choose a subset of $\{ A _ i \}$ whose size is less than or equal to $K$ so that, for each bit in $[0, M)$, there is at least one $1$ and one $0$.
Obviously, we use the inclusive-exclusive principle to write the answer as follows. \[ A = \sum _ {mask \in 2 ^ M} (-1) ^ {popcount(mask)} f(mask), \] where
$f(mask) = $ the number of choices where, for each bit $i$ where $mask _ i = 1$, the condition is not satisfied. For the bit $mask _ i = 0$, arbitrary.
Solution
The condition that “the condition is not satisfied” is equivalent to that the $A _ i$’s is equal in the viewpoint of masked by $mask$. Therefore, for each $mask$, we define map<int, ll> count; and we execute $count[A[i] \& mask] \mathbin{ {+} {+} }$. For each $[mask, cnt] \in count$, we execute
\[
res \mathbin{ {+} {=} } \begin{pmatrix} cnt \\ 1 \end{pmatrix} + \dots + \begin{pmatrix} cnt \\ K \end{pmatrix}.
\]
And don’t forget to add $1$ to $res$ as the empty set.
F - Triangles
Initial setting
We solve two problems $solve(H, W, K)$ and $solve(W, H, K)$. In addition, by symmetry of left and right, we fix that one vertex is on the left edge, one vertex is on the bottom edge and the other vertex is on the top edge. We set $x$, $y$ and $s$ as described in the following picture.
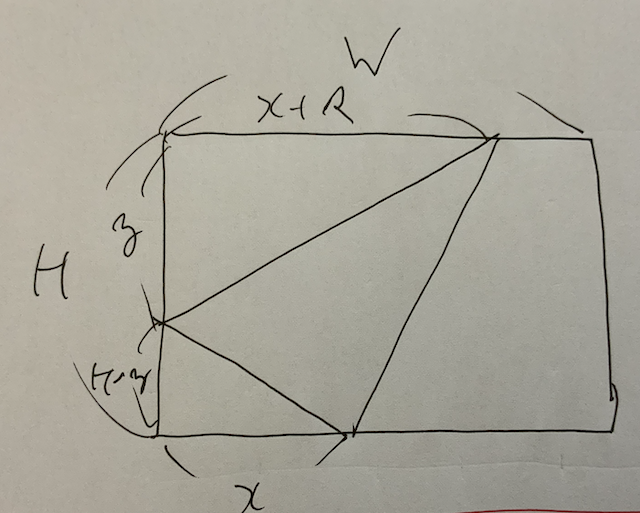
Here, we assume $s \geq 0$ as long as we double the result when $s > 0$ by the symmetry of bottom and top. The variables runs in $0 < x < W - 1$, $0 \leq s < W - 1$, $0 \leq s < W - x$ and $0 < y < H$.
Observation
Let $i$ be the number of the interior grid points. Let $b$ the number of the grid points on the edges including the vertexes. Let $S$ be the area of the triangle. By Pick’s theorem, we have the following relation.
\[
2S = 2i + b - 2.
\]
By direct calculation, we have the following equation.
\[
\begin{align}
2S &= H(2x + s) - (H - y)x - y(x + s) \\
&= Hx + s(H - y).
\end{align}
\]
It is well-known that we can count the grid points on the edges by $\gcd$ as follows.
\[
b = \gcd(H - y, s) + \gcd(y, x + s) + \gcd(s, H).
\]
Hence, the condition $i \leq K$ is equivalent to the following.
\[
2K \geq Hx + s(H - y) - \gcd(H - y, x) - \gcd(y, x + s) - \gcd(s, H) + 2 \tag{F.1}
\]
Solution
We fix $(s, y)$. The equation (F.1) is equivalent to the following. \[ Hx - \gcd(H - y, x) - \gcd(y, x + s) \leq 2K - s(H - y) + \gcd(s, H) - 2. \tag{F.2} \] Let $R(s, y) = 2K - s(H - y) + \gcd(s, H) - 2$ and $L(x, s, y) = Hx - \gcd(H - y, x) - \gcd(y, x + s)$.
Here, we see that $\gcd(H - y, x) + \gcd(y, x + s) \leq H$ since the left hand side is the sum of the number of the grid point on the two edge, which cannot exceed $H$. Hence,, (F.2) surely holds when $x \leq R(s, y) / H$ and does not when $x > R(s, y) / H + 1$. Thus we check (F.2) for just one possibility $x = R(s, y) / H + 1$ (or zero possibility if it is out-of-range) to decide the result is $\min(E / H, W - 1)$ or its plus one.
Then, we run $(s, y)$. Let $R _ {prep}(s, y) = 2K - s(H - y) + H - 2$. Then, it holds that
- $R(s, y) \leq R _ {prep}(s, y)$,
- $R _ {prep}$ is increasing for $y$ and decreasing for $s$.
We consider only for $(s, y)$ where $R _ {prep} (s, y) \geq 0$. Therefore, we run $y = 1, \dots, H - 1$ and $s = W - 2, \dots, 0$ as long as $R _ {prep} (s, y) \geq 0$.
