AtCoder Beginner Contest 167
Updated:
Source codes
Solutions
A - Registration
Execute T.pop_back(); and check if $S = T$ or not.
B - Easy Linear Programming
Do as they indicate us to. Use auto tmp{min(a, k)}; and execute a -= tmp; and k -= tmp;.
C - Skill Up
Apply brute-force method by bitwise-operation.
D - Teleporter
Solution
This is a problem about a functional graph. Assume $0$-indexed.
We start $0$ and then we will be involved in a cycle. We preserve when we visited $v$ in $visited[v]$. Let $t$ be the length of the cycle and $l$ be the steps we need to be involved that cycle. We update $visited$ and will see duplicated number $n$. We determine $t = n - visited[v]$ and $l = visited[v]$.
If $k \leq n$, we have found the answer. Otherwise, we update $k \gets (k - r) \% t + r$ and search $visited$ for the answer.
Another features
- We can determine $t$ in $O(1)$-space and $O(N)$-time by Floyd’s tortoise and hare.
- NOMURA Programming Competition 2020 D - Urban Planning
E - Colorful Blocks
Assume $0$-indexed.
Solution
Let $0 \leq x \leq \min(K, N - 1) = K$ be the number of the pairs of the same-colored adjacent blocks.
For each such pairs, we think of removing the right block. The number of ways of the removed blocks is $\begin{pmatrix} N - 1 \\ x \end{pmatrix}$. Here, note that we cannot remove the $0$-th block.
The $(N - x)$ remaining blocks is colored so that all of the adjacent blocks are differently colored. Therefore, the number of ways to color the remaining blocks is $M (M - 1) ^ {N - x - 1}$.
Hence, the answer is \[ \sum _ {x = 0} ^ K \begin{pmatrix} N - 1 \\ x \end{pmatrix} M (M - 1) ^ {N - x - 1}. \]
F - Bracket Sequencing
Solution
We regard ( as $+1$ and ) as $-1$. We regard each string $s _ i$ as a pair of numbers $(\delta _ i, m _ i)$, where $\Delta _ i$ is the resulting cumulated sum and $m _ i$ is the minimum value of constructive cumulated sums.
We think of connecting these strings. Let $X$ be the cumulated sum so far. We can connect $(\delta _ i, m _ i)$ if $X + m _ i \geq 0$. After that $X \gets X + \delta _ i$. In the final state, $X = 0$ is needed. Note that the final value of $X$ is not changed if we change the order of strings.
The following proposition gives us a solution.
Proposition F.1: The answer is “Yes” if and only if we arrange $(\delta _ i, m _ i)$ as follows.
- We divide $\{ (\delta _ i, m _ i) \}$ into two sets: \[ \begin{align} S _ + &= \{ (\delta _ i, m _ i) \mid \delta _ i \geq 0 \}, \\
S _ - &= \{ (\delta _ i, m _ i) \mid \delta _ i < 0 \}. \end{align} \tag{F.1} \]- We sort $S _ +$ in $m _ i$’s descending order.
- We sort $S _ -$ in $m _ i - \delta _ i$’s ascending order.
- Connect $S _ +$ with $S _ -$.
Proof of Proposition F.1
Lemma F.2: Assume that $\{ (\delta _ i, m _ i) \}$ satisfies the condition. Let $S _ +$ and $S _ -$ defined as (F.1), preserving the order in each set. We connect $S _ +$ with $S _ -$. After this change of order, it satisfies the condition, too.
Proof: For each $(\delta ^ - _ i, m _ i) \in S _ -$, let $J(i)$ be the number of $(\delta ^ + _ j, n _ j) \in S _ +$ where $(\delta ^ + _ j, n _ j)$ is originally put before $(\delta ^ - _ i, m _ i)$. For each $(\delta ^ + _ j, n _ j) \in S _ +$, let $I(j)$ be the number of $(\delta ^ - _ i, m _ i) \in S _ -$ where $(\delta ^ - _ i, m _ i)$ is originally put before $(\delta ^ + _ j, n _ j)$.
We have to check if, for any $(\delta, m) \in S _ + \cup S _ -$, it follows that $X + m \geq 0$ or not.
Let $(\delta _ j ^ +, n _ j) \in S _ +$. Then, we would like to verify the following. \[ X = \sum _ {0 \leq k < j} \delta _ k ^ +; \ \ \ \ X + n _ j \geq 0 \] From the assumption, it follows that \[ X’ = \sum _ {0 \leq k < j} \delta _ k ^ + + \sum _ {0 \leq k < I(j)} \delta _ k ^ -; \ \ \ \ X’ + n _ j \geq 0. \] This is because the order inside $S _ +$ is preserved. Therefore, this inequality is satisfied since $X’ \leq X$.
Let $(\delta _ i ^ -, m _ i) \in S _ -$. Then, we would like to verify the following. \[ X = \sum _ {0 \leq k < \lvert S _ + \rvert} \delta _ k ^ + \sum _ {0 \leq k < i} \delta _ k ^ -; \ \ \ \ X + m _ i \geq 0 \] From the assumption, it follows that \[ X’ = \sum _ {0 \leq k < J(i)} \delta _ k ^ + \sum _ {0 \leq k < i} \delta _ k ^ -; \ \ \ \ X’ + m _ i \geq 0 \] This is because the order inside $S _ -$ is preserved. Therefore, this inequality is also satisfied since $X’ \leq X$. We complete the proof.
Lemma F.3: Let $S _ +$ and $S _ -$ be defined as (F.1). Suppose that the order generated by connecting $S _ +$ and $S _ -$ satisfies the condition. We sort $S _ +$ by $m _ i$’s descending order and connect $S _ +$ with $S _ -$. Then, it also satisfies the condition.
Proof: For elements in $S _ -$, the condition is same, regardless of the order of $S _ +$. Let $S _ +$ be sorted as above. For each $i = 0, 1, \dots, \lvert S _ + \rvert - 1$, we show that $(\delta ^ + _ i, m _ i)$ is valid. Assume to the contrary that $(\delta ^ + _ i, m _ i)$ is not valid. Then, it holds that $X = \sum _ {0 \leq k < i} \delta ^ + _ k$; $X + m _ i < 0$. By assumption, it follows that $m _ k \leq m _ i$ for $k \geq i$. We go back to the original order. We take first $(i + 1)$ elements from $S _ +$. It contains $(\delta ^ + _ k, m _ k)$ with $k \geq i$. Let $(\delta ^ + _ k, m _ k)$ be first-appeared element of them in the original order. Then, it holds that $X’ \leq X$. Thus, we have the following. \[ X’ + m _ k \leq X + m _ k \leq X + m _ i < 0, \] which contradicts the fact that the original order satisfies the condition. We complete the proof.
Lemma F.4: Let $S _ +$ and $S _ -$ be defined as (F.1). Suppose that the order generated by connecting $S _ +$ and $S _ -$ satisfies the condition. We sort $S _ -$ by $m _ i - \delta _ i$’s ascending order and connect $S _ +$ with $S _ -$. Then, it also satisfies the condition.
Proof: We think of the reverse version of this problem. We reverse $s _ i$ and we regard ( as $-1$ and ) as $+1$. Note that this manipulation is equivalent to the manipulation that we reverse the chart of cumulated sum. Then, we see that $\delta _ i$ becomes $- \delta _ i$ and $m _ i$ becomes $m _ i - \delta _ i$.
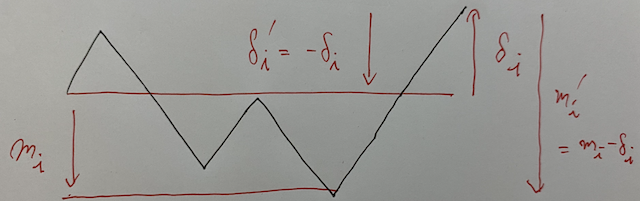
We apply Lemma F.4 for this version to see that we sort $S _ -$ in reversed-descending order of new $m _ i$, i.e., ascending order of $m _ i - \delta _ i$.
Proof of Proposition F.1: This is just a direct consequence from Lemmas F.2, F.3 and F.4.
