AtCoder Beginner Contest 165
Updated:
Source codes
Solutions
A - We Love Golf
Check is the largest multiple of $K$ less than or equal to $B$ is greater than or equal to $A$ or not, i.e., $(N / B) \times B \geq A$.
B - 1%
Just do the simulation. Use boost::multiprecision::cpp_int to prevent overflow. The calculation “$\times 1.01$” should be done by *= 101; and /= 100;.
C - Many Requirements
Apply brute-force method. The maximum number of possibilities will be $\begin{pmatrix} 20 \\ 10 \end{pmatrix} \approx 1.85 \times 10 ^ 5$.
We can construct the vector of the sequences of the length $n$ from that of the length $n - 1$ recursively.
D - Floor Function
Let $x = By + z$ with $y, z \in \mathbb{N}$ and $0 \leq z < B$. Then, we have
\[
\begin{align}
f(x) &= \left\lfloor \frac{Ax}{B} \right\rfloor - A \left\lfloor \frac{x}{B} \right\rfloor \\
&= \left\lfloor \frac{ABy + Az}{B} \right\rfloor - A \left\lfloor \frac{By + z}{B} \right\rfloor \\
&= Ay + \left\lfloor \frac{Az}{B} \right\rfloor - Ay \\
& = \left\lfloor \frac{Az}{B} \right\rfloor.
\end{align}
\]
This is an increasing function for $z$. Therefore, $\max _ {0 \leq x \leq N} f(x) = f(\min(B - 1, N))$.
E - Rotation Matching
Solution
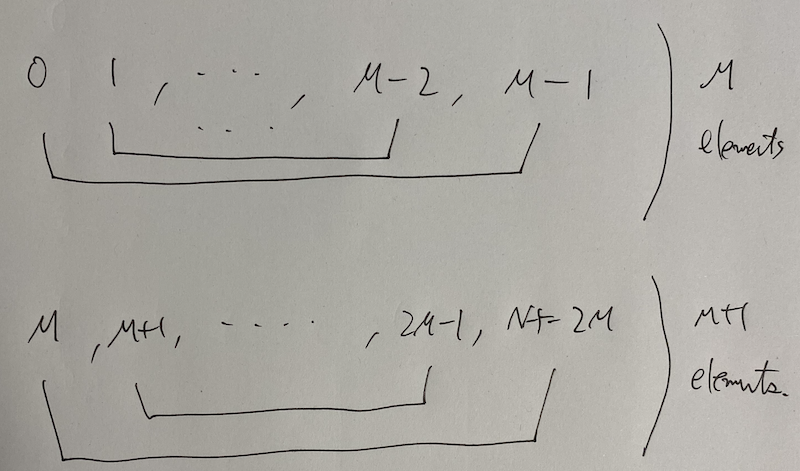
Assume $0$-indexed.
Consider the satisfying condition that $\{ (x _ i, y _ i) \} _ {i \in N}$ should be a valid allotment. The following condition is a satisfying condition. \[ \sharp \{ y _ i - x _ i, x _ i - y _ i \in \mathbb{Z} / N \mathbb{Z} \mid i \in M \} = 2M \tag{E.1} \]
We can assume that $N = 2M + 1$. The following picture gives an answer.
Implement
The following code gives an answer ($1$-indexed).
N = M * 2 + 1;
for (auto i{0}; i < M / 2; ++i)
{
cout << 1 + i << " " << M - i << endl;
}
for (auto i{0}; i < M - M / 2; ++i)
{
cout << M + 1 + i << " " << N - i << endl;
}
F - LIS on Tree
DP for the typical LIS
We recall the typical LIS. Assume that we calculate the length of the LIS on $\{ a[i] \} _ {i \in N}$.
Definition
We update the following table.
vector<int>$dp[i] = $ the minimum tail of the LIS of the length $(i + 1)$ in the current state.
Note that $dp$ is an increasing function of $i$.
Initial state
$dp[i] = \infty$.
Answer
The minimum index $i$ so that $dp[i] = \infty$. This is calculate by the following code.
lower_bound(dp.begin(), dp.end(), infty) - dp.begin();
Transition
For $i = 0, \dots, N - 1$, we find the minimum index $j$ so that $dp[j] \geq a[i]$ and $dp[j] \gets a[i]$. This is done by the following code.
*lower_bound(dp.begin(), dp.end(), a[i]) = a[i];
Solution
For each transition, we update just one line. Therefore, we can easily rollback in each step.
This is convenient for DFS. We use one LIS table and keep reusing it. When we come to the vertex, we do the transitions and calculation above. After visiting the children, we rollback it as follows.
void dfs(int src = 0, int parent = -1)
{
ans[src] = lis.query(a[src]);
for (auto const &e : v[src])
{
if (e.dst != parent)
{
dfs(e.dst, src);
}
}
lis.rollback();
}
