AtCoder Beginner Contest 163
Updated:
Source codes
Solutions
A - Circle Pond
Flush $2 \pi R$ with $\pi$ being M_PI.
B - Homework
Assume $0$-indexed.
The number of possible holidays is \[ X = N - \sum _ {i \in M} A _ i. \]
We flush $X$ if $X \geq 0$; otherwise -1.
C - management
We make the histogram of $A _ i$ and flush it.
D - Sum of Large Numbers
$10 ^ {100}$ is so large that this problem can be transformed into the following one.
Let $K \leq X \leq N + 1$. Choose $X$ elements from $\{ 0, 1, \dots, N \}$ and let $S$ be its sum. Then, how many possibilities of $(X, S)$ are there?
Assume $X$ is fixed. Then, the minimum of $S$ is \[ lb(X) = 0 + 1 + \dots + (X - 1) = \frac{X(X - 1)}{2}, \] wheres the maximum of $S$ is \[ ub(X) = N + (N - 1) + \dots + (N - (X - 1)) = NX - \frac{X(X - 1)}{2}. \] $S$ can be achieved any integers in $[lb, ub]$. Therefore, the answer is calculated as follows. \[ \sum _ {X = K} ^ {N + 1} \left( ub(X) - lb(X) + 1 \right). \]
E - Active Infants
Assume $0$-indexed.
Observation
Let $\sigma \in \mathfrak{S} _ N$. The score is described as follows. \[ f(\sigma) = \sum _ {i \in N} A _ i \lvert i - \sigma(i) \rvert. \] Here, we have the following relation about absolute value. \[ \lvert i - \sigma(i) \rvert = \max \{ i - \sigma(i), \sigma(i) - i \}. \] Hence, it follows that \[ f(\sigma) = \max _ {U \sqcup L = N} \left( \sum _ {i \in L} A _ i (\sigma(i) - i) + \sum _ {i \in U} A _ i (i - \sigma(i)) \right). \] What we want to find is \[ \max _ {\sigma \in \mathfrak{S} _ N} f(\sigma) = \max _ {U \sqcup L = N} \max _ {\sigma \in \mathfrak{S} _ N} \left( \sum _ {i \in L} A _ i (\sigma(i) - i) + \sum _ {i \in U} A _ i (i - \sigma(i)) \right). \] We fix the disjoint union $U \sqcup L = N$. How can we find the maximum argument of $\mathfrak{S} _ N$? Let $i, j \in U$ with $A _ i > A _ j$. If $\sigma$ gives its maximum, it follows that $\sigma(i) < \sigma(j)$, which is equivalent to \[ \left( A _ i (\sigma(i) - i) + A _ j (\sigma(j) - j) \right) - \left( A _ i (\sigma(j) - i) + A _ j (\sigma(i) - j) \right) = (A _ i - A _ j)(\sigma(i) - \sigma(j)) > 0. \] Thus, to summarize the situations, we have the followings.
- For any $i, j \in U$ with $A _ i > A _ j$, we have $\sigma(i) < \sigma(j)$.
- For any $i, j \in L$ with $A _ i > A _ j$, we have $\sigma(i) > \sigma(j)$.
Therefore, once we fix $U \sqcup L = N$, a greedy algorithm to determine $\sigma(i)$ in $A _ i$’s descending order works.
DP-part
Let $V = \{ A _ i, i \}$ be sorted in descending order.
Definition
vector<vector<ll>>$dp[i][j] = $ the possible maximum by determining $V[0, i)$’s places, with $\lvert U \rvert = j$.
Initial state
$dp[0][0] = 0$. Otherwise, $dp[i][j] = -\infty$.
Answer
$\max _ {0 \leq j \leq N} dp[N][j]$.
Transition
For $i = 0, \dots, N - 1$, let $(a, ind) = V[i]$. For $j = 0, \dots, N$, if $dp[i][j] = -\infty$, continue;.
We think both of the cases $ind \in U$ or $ind \in L$. For the former one, $\sigma(ind) = j$; for the latter one, $\sigma(ind) = N - 1 - (i - j)$. Hence, We execute the following two manipulations.
\[
\begin{align}
dp[i + 1][j + 1] &\gets ^ {\max} dp[i][j] + a (j - ind), \\
dp[i + 1][j] &\gets ^ {\max} dp[i][j] + a (N - 1 - (i - j) - ind).
\end{align}
\]
Actually, $j$ runs in $[0, i]$. Thus, the out-of-range problem will not occur.
F - path pass i
Assume $0$-indexed.
Basic strategy
We count the number of simple paths that won’t visit $k$-colored vertexes and subtract it from $N (N + 1) / 2$.
This number can be calculated by gathering the subgraphs generated by eliminating $k$-colored vertexes, more precisely, the sizes of them. Let $V _ k = \{ s _ 0, \dots, s _ l \}$ be the collection of its sizes. Then, what we want to calculate is $\sum _ {i = 0} ^ {l} s _ i (s _ i + 1) / 2$.
Solution (recursive DFS + colored stack)
We want to obtain $V _ k$ for all $k \in N$ in $O(N)$-time by DFS.
DFS
Consider the following graph, where black vertex is colored by $color$. We consider how to determine a subgraph $\{ 3 \}$ for this $color$.
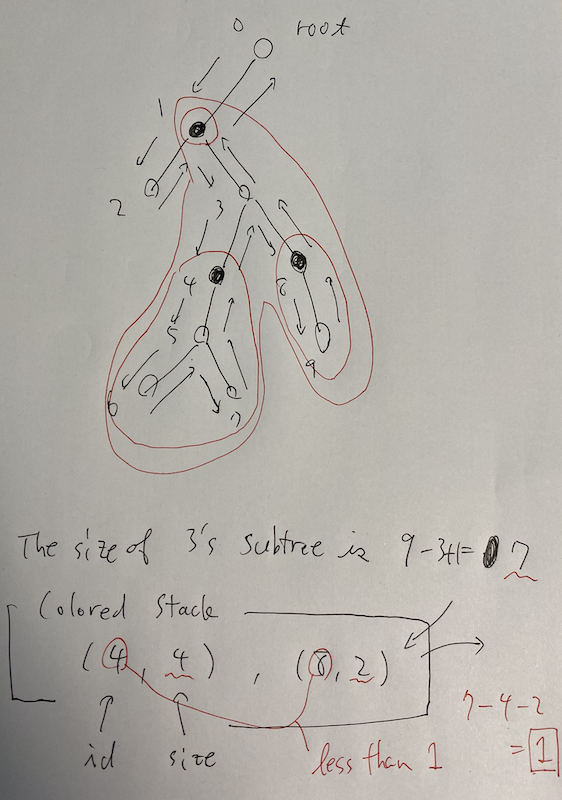
We use recursion and a vector of stacks $S$. Here, $S[color]$ has temporary subtrees that are not subtracted.
We give IDs for vertexes while visiting them. When the we visit back $3$ from $9$, we can determine the size of subtree $subtree$ whose root is $3$ by $9 - 3 + 1 = 7$. Then, we come back $1$ from $3$. We would like to get the size of the subgraph containing $3$ where $color$-colored vertexes are removed.
We look at $S[color]$, which are aligned by ids in descending order. Let $(id, size)$ be its top element. If $id$ is less than $1$, it means $subtree$ contains $(id, size)$, so we subtract $size$ from $subtree$’s size to obtain the size of the $color$-colored-removed subgraph.
Key Point
We have to get all $V[color]$ by one DFS. Thus, what we can use is restricted as follows.
- Information of DFS without color: going out and coming back.
- Colored stacks.
Other solution
We can use BIT or Segment tree instead of colored stack.
