AtCoder Grand Contest 043
Updated:
Source codes
Solutions
A - Range Flip Find Route
Observation
Consider the $1$-dimensional problem. Obviously, the answer is the number of the changes from white to black on that route.
Let’s go on to the $2$-dimensional problem. We fix a route. The answer must be greater than or equal to the number of the changes from white to black on that route. Here we count the constraint that we have to go in either right or down for each step. Therefore, it is impossible for the color changes to interfere with each other. Therefore, the obstacle is achieved by the number of the changes from white to black.
Solution
For non-fixed route version, we can solve this problem by DFS on the grid.
B - 123 Triangle
Let $A$ be the answer.
When does the answer become 2?
Lemma B.1: If the answer is $2$, each $a _ i$ is either $0$ or $2$.
Proof: Suppose that the answer is $2$. Consider the $n$-previous stage. We show this lemma by the induction on $n$. Obviously, it holds in the case $n = 0$. Suppose that it holds in the case $n$. Then, consider $(n + 1)$-previous stage. If $2$ is produced in $n$-th stage, the possible cases is $\lvert 0 - 2 \rvert$ or $\lvert 2 - 0 \rvert$. If $0$ is produced, the possible cases are $\lvert 0 - 0 \rvert$, $\lvert 1 - 1 \rvert$ or $\lvert 2 - 2 \rvert$. So we have to deny the case $\lvert 1 - 1 \rvert$. If all the numbers in $(n + 1)$-th are $1$, the $n$-th numbers are all $0$, which results in $0$ as the answer. Thus this is impossible. If all the numbers in $(n + 1)$-th are not necessarily $1$, but they contains $1$, there must be at least one calculation $\lvert 2 - 1 \rvert$ or $\lvert 1 - 0 \rvert$, which produce $1$. This contradicts the assumption on $n$. This completes the proof.
How about mod 2?
Lemma B.2: It follows that \[ A = \sum _ {i \in N} \begin{pmatrix} N - 1 \\ i \end{pmatrix} a _ i \text{ in } \mathbb{Z} / 2 \mathbb{Z}. \]
Proof: Since $\lvert x - y \rvert = x + y$ in $\mathbb{Z} / 2 \mathbb{Z}$, we can easily count the effect of $a _ i$ as $\begin{pmatrix} N - 1 \\ i \end{pmatrix}$.
Solution
If each $a _ i$ is either $0$ or $2$, we can convert $0 \mapsto 0$ and $2 \mapsto 1$ and apply Lemma B.2 to see whether $A$ is odd or even. If it is even, the real answer is $0$. If not, the real answer is $2$.
Otherwise, $A$ is either $0$ or $1$. We can determine this in $O(N)$-time by Lemma B.2.
We want to know each $\begin{pmatrix} N - 1 \\ i \end{pmatrix}$ is even or odd. This is easily done by counting the number of factors $2$ for each $k!$s.
C - Giant Graph
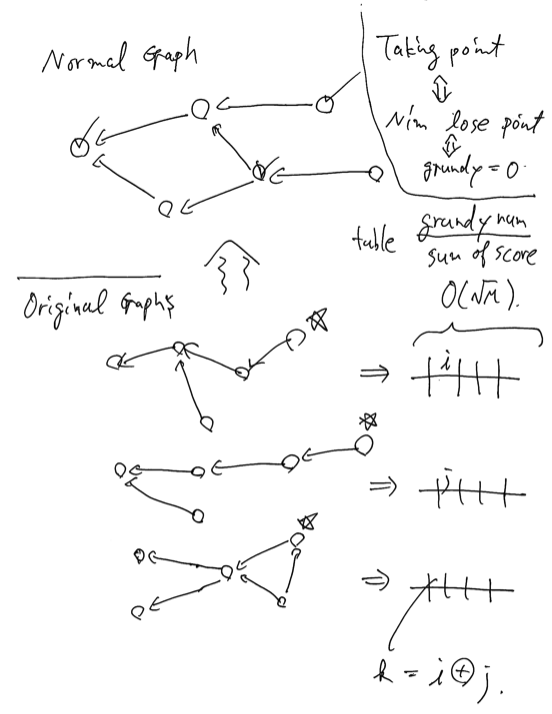
Initial observation
We focus on the huge constant $10 ^ {18}$. This is so large that we just apply the greedy method to make the largest stable set.
If the graph is normal, this greedy strategy is regarded as follows. We try all vertexes in the descending order. If we can take the vertex we visit, conquer it. Otherwise, don’t conquer it.
Nim and grundy number
This is equivalent to the famous Nim game. Suppose that the graph is directed where each edge is from the smaller number to the bigger number. We play moving piece game. There are two players. If a player cannot move the piece, they lose. Then, we can determine loser’s vertexes and winner’s vertexes. We conquer loser’s vertexes.
We move to the original there graphs. We can extend this idea by using a piece on each graph. Two players move these three pieces. What we have to consider is loser’s states. This is calculated by grundy number. Note that its score is calculated by $B ^ i \cdot B ^ j \cdot B ^ k$, where $B = 10 ^ {18}$.
Solution
For each graph, for all vertexes, we compute their grundy numbers. We can use unordered_set<int> S; and follow the definition of the grundy number to complete this task in $O(M)$-time. Then, create the table $T$ where
$T[i] = $ the sum of the scores in vertex whose grundy number is $i$.
Here we estimate the upper bound of the grundy number on a graph. Let $K$ be the largest grundy number. Then, considering the best possible case, it follows that \[ 1 + 2 + 3 + \dots + K = \frac{K(K + 1)}{2} \leq M. \] Therefore, it follows that $K \leq \sqrt{2M}$.
Let $T _ X$, $T _ Y$, and $T _ Z$ be the table above of the graph $X$, $Y$ and $Z$, respectively. We can try all pairs of the indexes $(i, j)$ in $O(M)$-time. Let $k = i \oplus j$. The answer is the sum of $T _ X[i] T _ Y[j] T _ Z[k]$.
D - Merge Triplets
Assume $1$-indexed.
Important idea: Block
First, we demonstrate the following case. \[ \{ 1, 6, 5 \}, \{ 3, 2, 4 \}. \] From this, we generate the following permutation. \[ 1, 3, 2, 4, 6, 5. \] Here we point out the number $6 = 3N$, the maximum number. When the top of the former queue is $6$, this queue is blocked until the others become empty. Therefore, the part $[6, 5]$ appears in the result as it is. We consider the blocks, each top of which is the maximum number having appeared before. In this case, we make blocks as follows. \[ \{ [1], [6, 5] \}, \{ [3, 2], [4] \} \] Then, the result is as follows. \[ [1], [3, 2], [4], [6, 5]. \]
Yes or No problem
Suppose that we are given a permutation $\{ p _ i \} _ {i = 1} ^ {3N}$. When can it be generated by our rule? Let’s consider it by examples in $N = 2$.
Example #1
\[ [1], [6, 4, 2, 3, 5] \] cannot be generated since it contains a $5$-length block. We cannot pack into a $3$-length sequence.
Example #2
\[ [1], [2], [4, 3], [6, 5] \] can be generated, for example, by the following sequences. \[ \{ [1], [4, 3] \}, \{ [2], [6, 5] \}. \]
Example #3
\[ [2, 1], [4, 3], [6, 5] \] cannot be generated since we cannot pack three $2$-length blocks into two $3$-length sequence.
Example #4
\[ [2, 1], [4, 3], [5], [6] \] can be generated, for example, by the following sequences. \[ \{ [2, 1], [5] \}, \{ [4, 3], [6] \}. \]
Example #5
\[ [2, 1], [3], [4], [5], [6] \] can be generated, for example, by the following sequences. \[ \{ [2, 1], [3] \}, \{ [4], [5], [6] \}. \]
Conclusion
The condition is as follows.
- There is no block whose length is greater than or equal to $3$.
- The number of $2$-length blocks $\leq$ the number of $1$-length blocks.
DP part
Let’s convert the ideas above into DP.
Definition
$dp[i][j] = $ the number of relatively magnitude relationships when we consider $[1, i]$ with the number of $1$-length blocks $-$ the number of $2$-length blocks.
Naively, we want to determine the number of $i$-th elements in order, but this idea does not work. Instead of possessing concrete numbers, we keep relatively magnitude relationships. This idea enables us to insert numbers later.
We don’t have to care the concrete numbers for each element in the middle of DP. They are automatically determine when we reach the last element.
Here, we have to care that $j$ moves in $[-N, 3N]$. Therefore, we use vector<vector<ll>> dp(3 * N + 1, vector<ll>(4 * N + 1)).
Initial state
We set $dp[0][0 + N] = 1$. Otherwise $0$.
Answer
\[ \sum _ {j = 0} ^ {3N} dp[3N][j + N]. \]
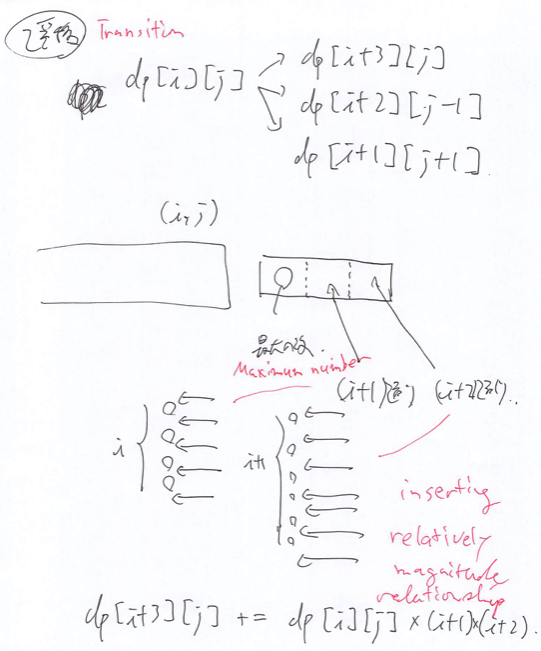
Transition
For $i = 0, \dots, 3N$, for $j = 0, \dots, 4N$, we execute the following.
\[
\begin{align}
dp[i + 3][j] & \mathbin{ {+} {=} } dp[i][j] \times (i + 1)(i + 2), \\
dp[i + 2][j] & \mathbin{ {+} {=} } dp[i][j] \times (i + 1), \\
dp[i + 1][j] & \mathbin{ {+} {=} } dp[i][j].
\end{align}
\]
Here, out-of-range transitions shall be ignored and modulo manipulations are omitted.
For example, We can see the last line by the following picture.
E - Topology
Fundamental group
Let $p _ i = (1/2 + i, 1/2)$ for $i = 0, \dots, N - 1$. We consider $X = \mathbb{R} ^ 2 \setminus \{ p _ 0, \dots, p _ {N - 1} \}$. Here, we have the following homotopic equivalence. \[ \mathbb{R} ^ 2 \setminus \{ p _ 0, \dots, p _ {N - 1} \} \simeq \bigvee _ {N} S ^ 1. \] Then, by van Kampen’s theorem, we have \[ \pi _ 1 (X) \cong (x _ 0 , \dots x _ {N - 1}). \tag{E.1} \] Here, the right hand side is the free group generated by the words $x _ 0, \dots, x _ {N - 1}$. Each $x _ i$ represents the homotopic equivalent set of the positive cycle whose center is $p _ i$. Since we use the knowledge of fundamental group, we see the followings.
- The chain $C \in \pi _ 1 (X)$ is homotopic to one point if and only if $[C] = e$ in $(x _ 0 , \dots x _ {N - 1})$.
For $i \in N$, let $f _ i \colon (x _ 0, \dots, x _ {N - 1}) \to (x _ 0, \dots, x _ {N - 1})$ be the homomorphism defined by $f _ i (x _ i) = e$ and $f _ i (x _ j) = x _ j$ for $i \neq j$.
- Suppose that we remove the point $p _ i$ from the set of the forbidden points. The chain $C \in \pi _ 1 (X)$ is homotopic to one point if and only if $f _ i([C]) = e$ in $(x _ 0 , \dots x _ {N - 1})$.
If we remove several points, we apply several corresponding homomorphism for $[C]$.
Important observation
Let $N = 2$ and $A = 1110$. How can we give this example? Let’s consider this problem in the viewpoint of fundamental group.
We consider (E.1) in $N = 2$. Therefore, the condition $A = 1110$ is equivalent to the task to find $g \in \ker f _ 0 \cap \ker f _ 1 \setminus \{ e \}$. But this is very easy. We can find the following element. \[ g = x _ 0 x _ 1 x _ 0 ^ {-1} x _ 1 ^ {-1}. \tag{E.2} \] In fact, $f _ 0 (g) = e x _ 1 e x _ 1 ^ {-1} = e$ and $f _ 1 (g) = x _ 0 e x _ 0 ^ {-1} e = e$ and $g \neq e$.
How about larger cases?
Let $N = 3$ and $A = 11111110$. How can we apply the idea of (E.2)? Let $g$ defined by (E.2). Then, the following element gives us an example. \[ h = g x _ 2 g ^{-1} x _ 2 ^ {-1}. \tag{E.3} \] In fact, we can check the facts $f _ i (h) = e x _ 2 e x _ 2 ^ {-1} = e$ for $i = 0, 1$ and $f _ 2 (h) = g e g ^{-1} e = e$ and $g \neq e$ to see that $h \in \ker f _ 0 \cap \ker f _ 1 \cap \ker f _ 2 \setminus \{ e \}$.
We can apply this idea for the larger cases by recursion.
Solution
Note that the constraints that $N \leq 8$ and that the number of points is less than or equal to $250,000$ are very loose. Thus we can implement in the easier way.
Before creating the path, we have to determine whether the answer is possible or not. If we have the pair of the set $(i, j) \in \mathcal{P}(N) \times \mathcal{P}(N)$ that satisfies $j \neq i$, $j \subset i$, $A _ j = 0$ and $A _ i = 1$, the answer is impossible. We can determine in $O((2 ^ {N}) ^ 2)$-time. In addition, if $A _ \emptyset = 1$, the answer is impossible. Otherwise, the answer is possible.
First, we create the path of the cycle $x _ i$ and $x _ i ^ {-1}$. To connect them in the further implementation, we set the start and end point as $(0, 0)$.
Next, we compose the chain of the cycles. We determine where to apply the technique above. For $i \subset N$ which satisfies $A _ i = 0$, we have to forbid the homotopic equivalence to the one point. But if we find $j \subset i$ that satisfies $j \neq i$ $A _ j = 0$, forbidding $j$ is suffice to forbid $i$. Otherwise, we apply the technique above. As we argued, we can compose this chain by the recursive method.
Just connecting the above chains, we obtain the desired chain.
Why is the judge valid?
According to the editorial and the YouTube live, the judge determine whether the given curve is correct or not by the following way. It initializes the queue and goes on the curve. When the curve passes the point $(1/2 + i, 0)$, the judge inserts $a _ i$ into the queue. When the curve passes the point $(1/2 + i, 1)$, the judge inserts $b _ i$ into the queue. After scanning the curve, the judge erase adjacent $a _ i a _ i$ and $b _ i b _ i$ in the recursive way. When it wants to remove $p _ i$, it just ignores $a _ i$ and $b _ i$. If the curve is homotopic to one point, the queue will be empty. Otherwise, not.
This algorithm always gives the correct judgement.
First, the trivial homotopic equivalence such as going and backing is canceled by the erasing rule of the same adjacent characters.
Second, if we replace $b _ i$ with $a _ i$, the queue will become empty since this is the projection into the $x$-axis of the closed curve. It means we can always find the adjacent $a _ i b _ i$ or $b _ i a _ i$ in the recursive way unless the queue is empty.
We convert this queue into $[C]$. We see the elements from top to the last. If we find $a _ i b _ i$, we erase them and write $x _ i$. If we find $b _ i a _ i$, we erase them and write $x _ i ^ {-1}$. We always find those until the queue become empty. The result is $[C]$.
If the curve $C$ is homotopic to one point, each cycle must be reduced by the rule $x _ i x _ i ^ {-1} = x _ i ^ {-1} x _ i = e$. In the original queue, they mean $a _ i b _ i b _ i a _ i$ or $b _ i a _ i a _ i b _ i$. But those words must have been erased by the rule above. Therefore, the queue must have been empty.
If the queue is empty, it means the closed curve kept going and backing. It is trivial to see the curve is homotopic to the starting point without topological viewpoints.
