AtCoder Beginner Contest 158
Updated:
- Review: 2020-06-19
Source codes
Solutions
A - Station and Bus
If the string is “AAA” or “BBB”, the answer is No. Otherwise, Yes.
B - Count Balls
Let $C = A + B$. The answer is given by \[ A \cdot (N / C) + \min(N \% C, A). \]
C - Tax Increase
Try all possibility. Roughly, it suffices to try $N \leq 10000$.
D - String Formation
Observation
We cannot reverse the string for each step. It will result in $O(Q (\lvert S \lvert + Q))$-time. Instead of reversing the string itself, we possess the direction of the string in the viewpoint of the original string. Let bool reversed; to be this direction.
Solution
Let stringstream prefix; be the reversed prefix and stringstream suffix; be the suffix.
When we encounter Query 1, we swap prefix and suffix. When Query 2, we add $C _ i$s into either of them as indicated to.
The answer part: If reversed, We reverse $S$. The answer is reversed prefix + $+ S +$ suffix.
Point
It is a good tip to swap prefix and suffix.
E - Divisible Substring
Solution
Let $X _ i = S[N - i, N)$ for $1 \leq i \leq N$ and $X _ 0 = 1$. We have to count $(i, j)$ so that $0 \leq i < j \leq N$ and \[ \frac{X _ j - X _ i}{10 ^ i} = 0 \text{ in } \mathbb{Z} / P \mathbb{Z}. \tag{E.1} \]
If $P = 2$ or $5$, this problem is easily solved since whether a number can be divided by $P$ or not depends only on the last digit.
If $P \neq 2, 5$, (E.1) is equivalent to $X _ j = X _ i$ in $\mathbb{Z}/P\mathbb{Z}$. Thus we just possess the table between the remainder and its count.
F - Removing Robots
Assume $0$-indexed. We sort the robots in descending order of its coordinate.
Be careful for $MOD = 998244353$ in this problem!
My solution
Observation
We determine what robots each robot makes activated by using set<tuple<ll, int>> S; or binary search. We consider $i$-th robot. Let $k$ be the minimum robot it makes activated, i.e., $i$-th robot makes $[k, i)$-th robots activated. They also makes other robots activated, but their calculations are done, by recursively. That is, writing its result for $j$-th robot as $f(j)$, we have the following equation.
\[
f(i) = \min _ {j \in [k, i)} f(j).
\]
This is calculated by segment tree for range minimum query, i.e., $tree[i] = f(i)$.
Therefore, if we activate $i$-th robot, it results removing $[f(i), i)$-th robots. The problem becomes that for $[0, f(i))$-th robots. If not, it becomes that for $[0, i)$-th robots of course. Hence, we can solve this problem by DP.
Definition
$DP[i] = $ the number of the possible resulting states for the smaller problem on $[0, i)$-th robots.
Initial state
$DP[0] = 0$.
Answer
$DP[N]$.
Transition
For $i = 0, \dots, N - 1$, we execute the following. \[ DP[i + 1] = DP[i] + DP[tree[i]]. \]
Solution in YouTube Live
Observation
We regard each robot as a vertex and each relation $(v, w)$ as $v$ directly activates $w$ as an edge. We consider this graph. This graph is DAG, since, for each $e = (v, w)$, it holds that $v > w$. The problem becomes as follows.
Problem F.1: Let $G = (V, E)$ be a DAG. We color each vertex for $0$ or $1$. For each $(v, w) \in E$, it is prohibited that $c(v) = 1$ and $c(w) = 0$. How many colorings are possible?
This problem can’t be solved in programming contests. Let’s find what property is there in this problem.
Reduce edges to make a forest
We see that we can remove an edge $(u, w)$ if there are two edges $(u, v)$ and $(v, w)$. We remove this type of the edges. We show the following lemma.
Lemma F.2: After removing the edges above, the graph becomes a forest.
Proof: We show that any vertex $v$ has at most one edge whose destination is $v$. Assume to the contrary that there are two edges $(u, v)$ and $(w, v)$ with $u > w$. Then, it holds that $u > w > v$. Existence of the edge $(u, v)$ means that the robot $u$ activates directly $v$. Therefore, before that, $u$ must have activated $w$. Thus, there exists an edge $(u, w)$. This is a contradiction, since, if it should happen, we must have erased the edge $(u, v)$. This completes the proof.
To make this resulting tree directly, we think of the source $i \in N$ in ascending order. We hold current roots set<tuple<ll, int>> S; and try to connect $i$ and $j \in S$. If we manage to connect, we erase $j$ from $S$ and proceed. Otherwise, break;.
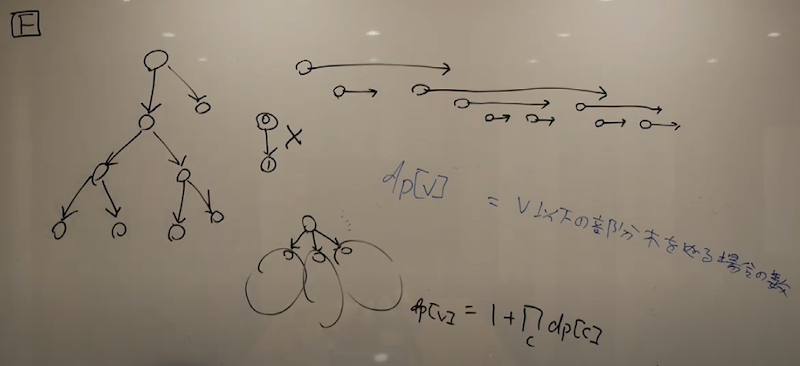
Solution
We calculate the following function.
mint$dfs(i) = $ the number of the valid colorings for the subtree whose root is $i$.
We have the following relation. \[ dfs(i) = 1 + \prod _ {j \in children(i)} dfs(j). \] Here, $1$ means the case we color $i$ as $0$, i.e., if we activate $i$-th robot, it results in the activation for all the robots in this subtree.
The answer is the product of $dfs(i)$ for $i \in S$.
Others
Real-time:
A - sample: 3, tle: 2.000, time: 01:18, from_submit: 98:01
B - sample: 3, tle: 2.000, time: 01:37, from_submit: 96:24
C - sample: 3, tle: 2.000, time: 02:35, from_submit: 93:49
D - sample: 3, tle: 2.000, time: 11:49, from_submit: 82:00
E - sample: 3, tle: 2.000, time: 43:00, from_submit: 39:00
F - sample: 4, tle: 2.000, time: 39:00, from_submit: 00:00
Review 2020-06-19:
A - sample: 3, tle: 2.000, time: 04:42, from_submit: 86:31
B - sample: 3, tle: 2.000, time: 04:10, from_submit: 82:21
C - sample: 3, tle: 2.000, time: 00:05, from_submit: 82:16
D - sample: 3, tle: 2.000, time: 09:59, from_submit: 72:17
E - sample: 4, tle: 2.000, time: 37:47, from_submit: 34:31
F - sample: 4, tle: 2.000, time: 34:31, from_submit: 00:00
