AtCoder Beginner Contest 155
Updated:
- Review: 2020-06-17
Source codes
Solutions
A - Poor
We get the input by vector<int> A(3);. We sort it. The answer is Yes if either of the following holds.
- $A[0] = A[1]$ and $A[1] \neq A[2]$,
- $A[0] \neq A[1]$ and $A[1] = A[2]$.
B - Papers, Please
If we find such $A$ that
\[
A \% 2 = 0 \land A \% 3 \neq 0 \land A \% 5 \neq 0,
\]
the answer is No. Otherwise, Yes.
C - Poll
We define map<string, int> M; and we gather the poll papers. Then, we get the maximum of the number of votes. We again search $M$ for the strings that are written on the maximal number and flush them. They are automatically in lexicographical order.
D - Pairs
Observation
The answer is the maximum value of $X$ so that there is less than $K$ pairs whose product is less than $X$. This is a problem for us to use binary search for $X$.
We divide this problem into three cases.
- The answer is negative.
- The answer is zero.
- The answer is positive.
Therefore, we split $A$ into there vectors $plus$, $zero$, $minus$. We can ignore $zero$. Let $P = \lvert plus \rvert$ and $M = \lvert minus \rvert$. Let $S _ p$, $S _ z$ and $S _ m$ be the numbers of the positive, zero, and negative pairs, respectively. We see that $S _ p = P (P - 1) / 2 + M (M - 1) / 2$, $S _ m = PM$ and $S _ z = N (N - 1) / 2 - S _ p - S _ m$. Then, we now know the division into cases as follows.
- The answer is negative if $K \leq S _ m$.
- The answer is zero if neither 1. or 3. holds. In this case, flush $0$ immediately.
- The answer is positive if $K > S _ m + S _ z$. In this case, we fix $K \gets K - (S _ m + S _ z)$.
Solution
Case: Negative
We solve the case 1. We are going to solve this problem by binary search for the answer. We need a judge function.
$count(T) = $ the number of the pairs whose product is less than $T$.
This is the sum of the following function with $x \in minus$.
$count(T, x) = $ the number of the elements $y \in plus$ so that $xy$ is less than $T$.
We sort $plus$ in descending order and $minus$ in ascending order in advance. We can compute this function by binary search for the index of $plus$.
Case: Positive
Similar solution works for the case 3. We sort $plus$ in ascending order and $minus$ in descending order in advance. We mend the solution above by the following function.
$count(T, i, V) = $ the number of the elements $V[j]$ with $j > i$ so that $V[i]V[j]$ is less than $T$.
Time complexity
The total time complexity will be $O((\log L) N \log N)$, where $L$ is the possible maximum value for this problem.
E - Payment
Observation
Suppose that we pay for “…3”. How many coins of $1$-denomination are used?
If both the customer and the shop uses at least one $1$-denomination, it is not the best strategy since they both reduce at least one $1$-denomination.
Hence, there are two possibilities for each digit.
- The customer uses the denomination and the shop won’t pay back.
- The customer does not use the denomination and the shop pay back.
For the former case, the customer uses three $1$-denomination. For the latter case, the shop pay back seven $1$-denomination. In this case, the customer will use one more $10$-denomination. Thus, in the digit-DP, we possess this state as well.
Solution: Digit-DP
First, we reverse the string and let $N$ be the length of it.
Definition
$dp[i][j] = $ the minimum number of the coins considering $S[0, i)$. Here, $j = 0$ means that there is no moving up; $j = 1$ means that there is.
Initial state
$dp[0][0] = 1$. Otherwise, $\infty$.
Answer
$\min(dp[N][0], dp[N][1] + 1)$.
The latter case occurs when, for example, we pay $9,999$ yen and we use one $10,000$-yen bill.
Transition
We will mean by $k = 0$ that we will resolve moving-up and by $k = 1$ that we won’t.
For $i \in N$, for $j = 0, 1$, for $k = 0, 1$, let $ni = i + 1$ and $nj = k$. We execute the following. \[ dp[ni][nj] \gets \min(dp[ni][nj], dp[i][j] + cost). \] Here, we determine $cost$ as follows.
- If $j = 0$ and $k = 0$, of course we set $cost = d$.
- If $j = 0$ and $k = 1$, we set $cost = 10 - d$ as we have discussed.
- If $j = 1$ and $k = 0$, we set $d + 1$. We can ignore $d = 9$, but don’t have to.
- If $j = 1$ and $k = 1$, we see that $cost = 10 - d - 1$. If we pay $9,999$ yen by one $10,000$-yen bill, we won’t use $1$, $10$, $100$, $1000$-denominations at all.
F - Perils in Parallel
Preparation
We can put the bombs in the array $A$ whose index starts by $0$ and ends by $N - 1$. The key $i$ manipulates $[l _ i, r _ i]$-bombs for $i \in M$. We can use lower_bound(bombs.begin(), bombs.end(), Bomb{l, -1}); to find $l$.
Observation
This problem is about range-xor. Therefore, we make difference-xor as follows. $B[0] = A[0]$ and $B[i] = A[i - 1] \oplus A[i]$ for $i = 1, \dots, N$. To implement, it may be safer to make $B[N] = A[N - 1]$.
Our objective is to make all $A[i]$ into $0$. This is equivalent to that all $B[i]$s are $0$. In the viewpoint of $B$, The key $[l, r]$ works for $\{ l, r + 1 \}$.
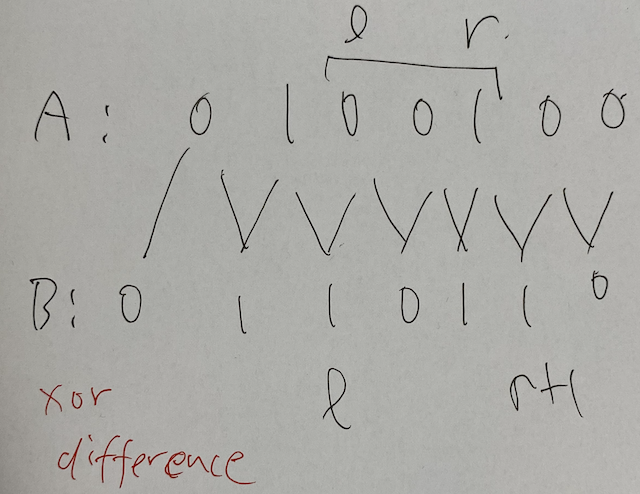
Then, we can regard each key as an edge connecting the vertex $l$ and $r + 1$. Hence, the problem has become as follows.
Problem F.1: We are given a graph $(V, E)$. Each vertex has a value in $\mathbb{F} _ 2$. Can we put a value in $\mathbb{F} _ 2$ on each edge so that the following holds for any vertex $v \in V$? \[ value(v) + \sum _ {e \in E _ v} value(e) = 0 \in \mathbb{F} _ 2. \tag{F.1} \]
Solution
We work on each connected component. If the sum of the value of $v$ is $1 \in \mathbb{F}$, the answer is -1.
Otherwise, actually we can switch off all the bombs in this component. We take a spanning tree of this component. We work from the leaves to the root. If (F.1) is not satisfied yet, we put $1$ on the edge connecting $v$ and its parent. Otherwise, we put $0$. Then, (F.1) automatically follows for the root, too since the parity is valid.
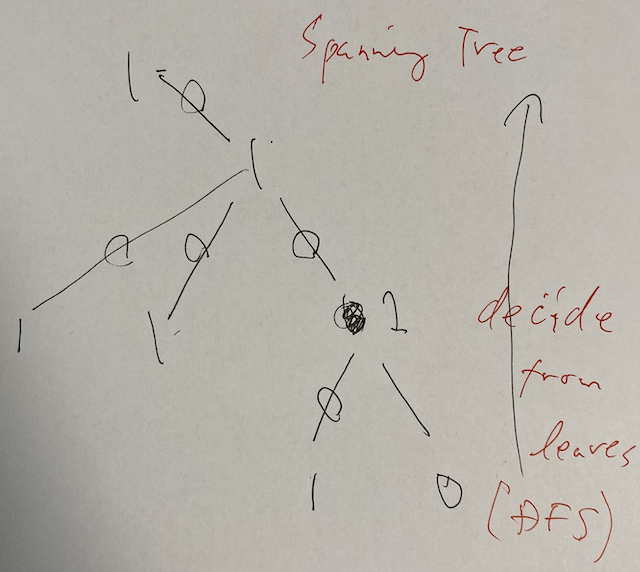
Key points
- Range-xor should be interpreted as difference-xor.
- Manipulation for two objects should be interpreted as an edge on a graph.
- Find one good way for a general graph by considering a (minimum) spanning tree for each connected component.
