Dwango Programming Contest 6th
Updated:
Source codes
Solutions
A - Falling Asleep
Just do as they indicate.
B - Fusing Slimes
Assume $0$-indexed.
Solution
Let $y _ i = x _ {i + 1} - x _ i$ for $i \in (N - 1)$. We count how many times we add $y _ i$ in terms of the expected value. This does not depend on the value of $y _ i$, just $i$. So we use $C _ i$ to denote this count.
Obviously, $C _ 0 = 1$. We make a recursive form of the relation between $C _ i$ and $C _ {i - 1}$.
Case 1
First we choose $i$. Then a slime runs on $y _ i$. The rest count will be equal to $C _ {i - 1}$. This probability is $1 / (i + 1)$.
Case 2
Otherwise, first choose will not effect on $y _ i$. The rest count will be equal to $C _ {i - 1}$ since there are $i$ slimes.
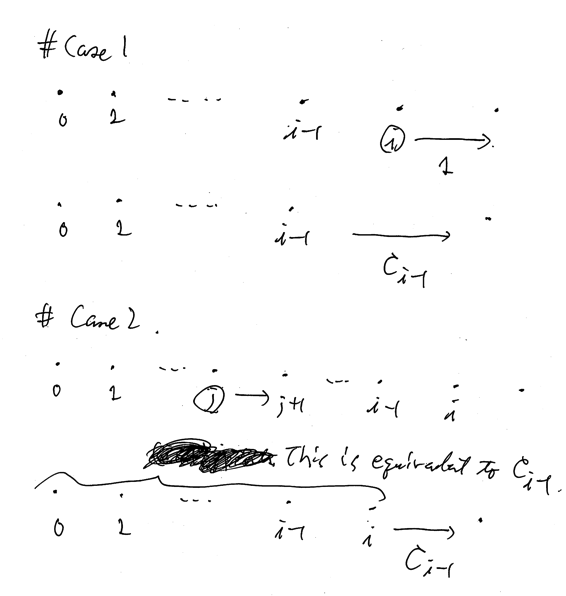
Summing up these results, we have the following recursive form.
\[ C _ i = \frac{1}{i + 1} (C _ {i - 1} + 1) + \frac{i}{i + 1} C _ {i - 1} = C _ {i - 1} + \frac{1}{i + 1}. \]
Then, $C _ i$ will be the harmonic sum. This will be directly calculated. The answer is \[ (N - 1) ! \sum _ {i = 0} ^ {N - 2} C _ i y _ i. \]
C - Cookie Distribution
Assume $0$-indexed.
Solution
First we consider what $H = c _ 0 \cdot \dots \cdot c _ {N - 1}$ means. For each $i$, we choose one cookie in each $c _ i$. The possibility is $H$. We color it by chocolate black, otherwise white.
Then, we change the order of the distribution and the coloring. We distribute black and white cookies to the children.
DP part
Definition
$dp[i][j] = $ the number of the possibilities of the cookies distributed for children in days $d \in i$ where $j$ black cookies having been distributed for $j$ children.
Initial State
We set $dp[0][0] = 1$; otherwise $0$.
Answer
$dp[K][N]$.
Transition
For $i = 0, \dots, K - 1$, for $j = 0, \dots, N$, for $k = 0, \dots, N - j$, we consider $dp[i][j] \mapsto dp[i + 1][j + k]$. First we consider $k$ black cookies. We choose $k$ people in the $N - j$ people who have not received black cookies yet. Then we choose $a _ i - k$ people in the $N - k$ people who will receive white cookies within this day. Therefore, the transition will be as follows. \[ dp[i + 1][j + k] \mathbin{ {+} {=} } dp[i][j] \times \begin{pmatrix} N - j \\\ k \end{pmatrix} \begin{pmatrix} N - k \\\ a _ j - k \end{pmatrix}, \] where the out-of-range means $0$.
