第一回日本最強プログラマー学生選手権-予選-
Updated:
Source codes
Solutions
A - Takahashi Calendar
模範解答
$2 \leq x, y \leq 9$ を充たす $(x, y)$ の組のうち、 $10x + y \leq D$ かつ $xy \leq M$ を充たす組の個数を求めればよろしい。
ポイント
この言い換えそのものをしなくて時間ロスしてしまった。
B - Kleene Inversion
解答
一つのブロックの中での真の意味での転倒数を $p$ とする。また、ブロックの中で順番を気にせず大きいものと小さいものを選んだ組の数を $q$ とする。答えは以下である。
\[ pK + q \frac{K (K - 1)}{2}. \]
ポイント
こうやってはっきり条件を整理するとわかりやすい。
C - Cell Inversion
模範解答
$0$-indexed とする。 $N \gets 2N = \lvert S \rvert$ としておく。
まず反転の条件を言い換える。 $0 \leq p < q < N$ に対し、区間 $[p, q]$ を反転させるとは、次を全て行うことと同値である。また実行する順番も最終結果には関係がない。
- 区間 $[0, p)$ を反転させる。
- 区間 $[0, q)$ を反転させる。
- マス $q$ を反転させる。
よって、全てのマスをちょうど $1$ 回ずつ選ぶということは、上の $2$ つは実行の詳細に依存せず実行されてしまう。だからまずこれらを実行する。この時点で黒のマスの個数と白のマスの個数が $N / 2$ でなければその時点でアウトで答えは $0$ である。
あとは場合の数を数えるだけである。 $ans = 1$ とする。カウンタ $c = 0$ を持っておき、前からみてって、白マスがきたら $c \mathbin{ {+} {=} } 1$ とする。黒マスがきたら $ans \mathbin{ {\times} {=} } c$ とし $c \mathbin{ {-} {=} } 1$ とする。途中で $0$ がかかった場合も答えが $0$ になって問題ない。
最後に選ぶ順番を考慮に入れて、答えは $ans \times (N/2)!$ である。
ポイント
同じ処理は $2$ 回やっていい場合は、半開区間に分ける。 これが良さそう。
D - Classified
頂点もレベルも $0$-indexed とする。
解答
$N - 1$ の最大 bit を $L$ とすると、レベル $L$ が最善である。その構成は、レベル $l = 0, \dots, L$ に対し、頂点 $i = 0, 1, \dots, N - 1$ に対し、 $j = i + 1, \dots, N - 1$ に対し、 $(i, j)$ をすでに結んでいなくて、かつ $i$ の $l$ 桁目 bit と $j$ の $l$ 桁目 bit が等しくない場合は、 $(i, j)$ をレベル $l$ で結ぶ。これで答えがでる。
解答の正当化
まず次の定理は既知とする。
定理 D.1:向きなしグラフについて、任意の頂点から任意の辺をいくつか通って頂点に戻るとき辺を通る回数が必ず偶数になることは、グラフの各連結成分が二部グラフであることと同値である。
つまりこの問題は、完全グラフを構成するために、二部グラフがいくつ部分グラフとして必要ですか、という問題である。まず次を示す。
補題 D.2:解答の構成で得られたグラフは、任意のレベルについての部分グラフを考慮すると、各連結成分が二部グラフになっている。
証明:レベル $l$ の部分グラフで出現する辺は、 $l$ 桁目同士が等しくないもの頂点同士を結んでいるので、二部グラフになっている。
次を示せば証明が終わる。
補題 D.3: $K \in \mathbb{N}$ とする。レベル $0, \dots, K$ の二部グラフの union として完全グラフが構成できるためには、 $N \leq 2 ^ {K + 1}$ が必要である。
証明:レベル $k$ の二部グラフの頂点を $c = 0, 1$ で塗り分けることにする。これらの union として完全グラフが得られたと仮定する。すると頂点 $i$ についてレベルごとの塗り分け方を並べたものを $V _ i = (c _ 0, c _ 1, \dots, c _ K)$ と書くことにする。もし $i \neq j$ が存在し $V _ i = V _ j$ となっているとすると、 $(i, j)$ を結ぶ二部グラフのレベルが実際には存在しないことになる。これは完全グラフであることに反する。すなわち $i = 0, \dots, N - 1$ に対し、 $V _ i$ たちは全て異なっていなくてはならない。 $V _ i$ たちの場合の数は $2 ^ {K + 1}$ であるので、つまり $N \leq 2 ^ {K + 1}$ である。
ポイント
条件を整理していくと証明にもなっている。
E - Card Collector
解答の方針
$0$-indexed とする。 $I _ i = (A _ i, R _ i, C _ i + H)$ を降順に sort する。ここで $I _ i$ を「頂点 $R _ i$, $C _ i + H$ を結ぶコスト $A _ i$ の辺」とみなす。このグラフでまず実現可能なグラフの条件を考察する。次にどのようにしてコストを最大化できるか考察する。最後に実装方法を示す。
実現可能なグラフ
このグラフにおいて、実際に操作で選べる辺の条件を考察する。各連結成分において、木または木に $1$ 本追加したものは、サイクルを $1$ つ含むがこれは可能である。その理由:このサイクルに一方向に向き付けをし、残りの枝は葉に向かって向き付けをするものとする。すると出口になった頂点でこの辺に相当するカードをとると、可能であることがわかる。逆にそれ以上辺が追加されると、このようなことはできない。その理由は、頂点の数が辺の数より小さいからである。
コストの最大化の仕方
そこで、コストを最大化するためには、クラスカル方の要領で貪欲に順番に $I _ i$ を検討していけばいいとわかる。つまり $I _ i = (A _ i, p _ i, q _ i)$ のとき、 $p _ i$ と $q _ i$ を含む部分が連結でないなら採用し、また、連結であってもまだ木である場合は採用する。これで答えが出る。
その理由は場合分けが発生するものの、クラスカル法の証明とほぼ同じである。見ていった辺の数の帰納法による。目の前の辺を採用できるのに採用しなかったのに、最大のグラフが構成できたとする。するとその最大のグラフに今の辺を追加して木 $+1$ になる場合は今の辺を追加できるので最大性に反する。よってその時点で木 $+1$ である。今の辺を使用しなかったのにこのグラフを構成できたなら、それに今の辺を追加して、今の辺以降に追加された辺のどれかを切れば木 $+1$ にすることが、どの場合でも可能である。
実装の方針
ほぼほぼクラスカル法と同様であり、 Union-Find を用いればいい。ただし木と木 $+1$ をどのようにして見分けるのかがポイントとなる。うまいやり方は Union-Find に $T = H + W$ という頂点を追加し、連結成分が木 $+1$ になったらその連結成分と $T$ を merge する。 ほぼクラスカル法の要領で進めるが、 $(p _ i, q _ i)$ が connected でない場合は採用して merge する。次に $(p _ i, q _ i)$ が connected である場合は $(p _ i, T)$ が connected であるかどうかを問い合わせる。 connected でない場合は、 $p _ i, q _ i$ を含む成分はまだ木であるので、そこにこの辺を追加することができる。そして $p _ i$ と $T$ を merge する。これで上記のアルゴリズムの実装となり、うまくいく。
ポイント
「頂点」を追加し「目印」にする。 グラフでよくあるあれと同じである。
補足:マトロイドによる正当化
今回の問題ではマトロイドを知っていると議論が単純化されるとのことなので、調べた。
マトロイドの定義
定義 E.1:$M = (S, \mathcal{I})$ が マトロイド であるとは、以下の (i)-(iii) を充たすことをいう。
(i) $S$ は有限集合であり、 $\mathcal{I} \subset \mathcal{P}(S)$ かつ $\mathcal{I} \neq \emptyset$ である。
(ii) $\mathcal{I}$ は 遺伝的 である。すなわち、 $A, B \subset S$ が $A \subset B$ かつ $B \in \mathcal{I}$ ならば $A \in \mathcal{I}$ である。
(iii) $M$ は 交換性 を持つ。すなわち、 $A, B \in \mathcal{I}$ に対し $\lvert A \rvert < \lvert B \rvert$ ならば、 $x \in B \setminus A$ が存在し、 $A \cup \{ x \} \in \mathcal{I}$ が成立する。
また、このとき $\mathcal{I}$ を $S$ の 独立部分集合族 といい、 $\mathcal{I}$ の元を 独立部分集合 という。
今回の場合
まず rng さんの言葉を使うことにする。
定義 E.2: $G = (V, E)$ を向きなしグラフとする。
- $G$ が 木 であるとは、 $G$ が連結であり $\lvert E \rvert = \lvert V \rvert - 1$ が成立することをいう。
- $G$ が 杏 であるとは、 $G$ が連結であり $\lvert E \rvert = \lvert V \rvert$ が成立することをいう。これは俗称である。普通は pseudotree というそうである。
- $G$ が 木または杏からなる森 であるとは、 $G$ の各連結成分が木または杏であることをいう。普通は pseudoforest というそうである。
今回の場合は、次を示せば、後の議論は後で述べる一般論から従う。
補題 E.3: $G = (V, E)$ を向きなしグラフとする。 $G$ の木または杏からなる森の辺集合全体を $\mathcal{I}$ とかく。このとき $M = (E, \mathcal{I})$ はマトロイドである。
この補題を示すために、次の補題をまず示す。
補題 E.4: $G = (V, E)$ を木または杏からなる森とする。このとき、 $G$ の(杏ではない)木の個数は、 $\lvert V \rvert - \lvert E \rvert$ 個である。
証明: $E$ に適当に順番をつけて、 $(V, \emptyset)$ に辺を追加していくことにする。このときまず最初の時点では $G$ の(杏ではない)木の個数は、 $\lvert V \rvert - \lvert \emptyset \rvert = \lvert V \rvert$ 個であるから主張は正しい。新たに $e \in E$ を加える時に、グラフがどうなるか考察する。このとき $e$ は異なる木同士を結ぶ、または木を杏に変える。よって $G$ の(杏ではない)木の個数は、 $e$ を追加することにより何れにしても $1$ 減ることになる。よって最終的にできるグラフ $G$ における木の個数は $\lvert V \rvert - \lvert E \rvert$ 個である。
補題 E.3 の証明:定義 E.1 の (i)-(iii) を示す。 (i) は自明である。まず (ii) を示す。 $A, B \subset E$, $B \in \mathcal{I}$ であるとする。このとき $A$ は $B$ から辺をいくつか削除したものであるから $A$ もまた木または杏からなる森の辺集合である。つまり $A \in \mathcal{I}$ である。次に (iii) を示す。 $A, B \in \mathcal{I}$ を $\lvert A \rvert < \lvert B \rvert$ なるものとする。このとき補題 E.3 により、 $A$ からできる森 $G _ A$ の方が $B$ からできる森 $G _ B$より、木の数が多いことになる。したがって、次のいずれかが起こっている。
- $G _ B$ のある木 $T$ が存在し、 $T$ の頂点が $G _ A$ の $2$ つ以上の木に属している。
- $G _ B$ のある杏 $T$ が存在し、 $T$ の頂点が $G _ A$ の $1$ つ以上の木に属している。
上の場合は、 $T$ は連結なので、 $G _ A$ の $2$ つの木を結ぶ辺 $e$ が存在する。このとき $A \cup \{ e \}$ は木と木を結んだだけなので、木または杏からなる森であることは保たれている。よって $A \cup \{ e \} \in \mathcal{I}$ である。また、下の場合は、 $G _ A$ の $2$ つの木を結ぶ辺 $e$ が存在する場合は上に帰着する。ない場合を以下では考察する。 $T$ の頂点は $G _ A$ のある木 $T’$ には属しているという仮定から、 $T$ の辺で、少なくとも片方の頂点が $T’$ に属している辺が存在する。このような辺を全て集めてきて、 $A$ に含まれているか考えてみると、全部は含まれていないはずである。というのも、全部が $A$ に含まれているならば、 $T’$ が木であることまたは $T$ が杏であることに反するからである。よって、$G _ A$ の別の杏に $T’$ が繋がれている辺 $e _ 1$ または $T’$ の頂点同士を繋いで杏にする辺 $e _ 2$ が存在し、 $e _ i \in B \setminus A$ である。これを $A$ に付与すると $A \cup \{ e _ i \} \in \mathcal{I}$ が成立する。以上で、補題は示された。
マトロイドの一般的性質
ここまでくればあとは一般論に任せられる。事実は書くが、詳細は文献を参照していただきたい。
定義 E.5: $M = (S, \mathcal{I})$ をマトロイドとする。
- $A \in \mathcal{I}$ とする。 $x \in S \setminus A$ が $A$ の 拡張 であるとは、 $A \cup \{ x \} \in \mathcal{I}$ であることをいう。
- $A \in \mathcal{I}$ が 極大 であるとは、 $A$ が拡張を持たないことをいう。
定理 E.6: $M = (S, \mathcal{I})$ をマトロイドとする。 $M$ の任意の極大部分集合のサイズは等しい。
証明の概略: $2$ つの極大部分集合のサイズが違う場合、交換性を用いて小さい方の極大性に矛盾がでる。
定義 E.7: $M = (S, \mathcal{I})$ をマトロイドとする。 $w \colon S \to \mathbb{N} _ +$ が与えられているとき、 $M$ は 重みづけられている という。 $A \subset S$ に対し、 \[ w(A) = \sum _ {x \in A} w(x) \] とすることで $w \colon \mathcal{P}(S) \to \mathbb{N} _ +$ に拡張する。このとき $w$ の $\mathcal{I}$ における制限に対し、 $w$ の最大値を与える $A \in \mathcal{I}$ を、 $M$ の 最適部分独立集合 という。
$w$ は正値関数であることから、$M$ の最適部分独立集合は、極大部分集合である。また、 マトロイドには要するにクラスカル法のアルゴリズムが使える 。つまり、 $A \gets \emptyset$ とする。$S$ を $w$ の降順でソートする。 $x \in S$ に対し、 $A \cup \{ x \} \in \mathcal{I}$ ならば $A \gets A \cup \{ x \}$ とするのを繰り返す。すると最終結果の $A$ は $M$ の最適部分独立集合になっている。この証明は省く。
以上でこの問題の解答が正当化された。
参考文献
以下の本の 16.4 節を参考にし、以上のエントリを書きました。
補足
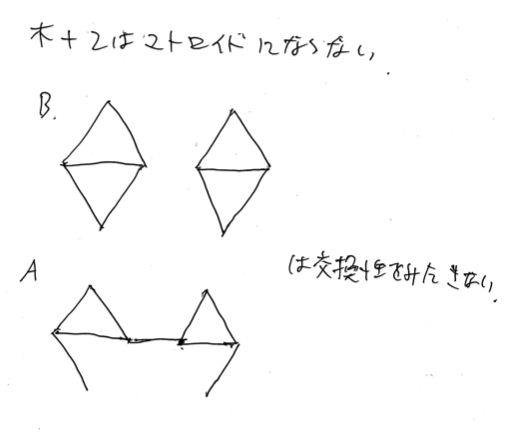
マトロイドになるのは、木だけの森、および、木+杏の森までっぽい。木 $+2$ までを許した森では、交換性が成り立たない反例が見つかった。
F - Candy Retribution
Sub-problems
Let’s convert this problem into sub-problems which we can solve easily. Now we count the number of $(A _ 0, \dots, A _ {N - 1}) \in \mathbb{N}^N$ with the sum $\leq R$ in which the $K$-th greater number is equal to the $(K + 1)$-th greater number. We use $f(R)$ to denote this number. The final answer is $f(R) - f(L - 1)$.
We once forget the “$K$-th $= (K + 1)$-th” condition to obtain the count as \[ \begin{pmatrix} R + N \\\ N \end{pmatrix}. \tag{F.1} \] This can be easily seen. For each $(A _ 0, \dots, A _ {N - 1})$ with $A _ 0 + \dots + A _ {N - 1} \leq R$, let $A _ N = R - (A _ 0 + \dots + A _ {N - 1})$ and instead of that just count $(A _ 0, \dots, A _ N)$ with $A _ 0 + \dots + A _ N = R$. Therefore, we count “$K$-th $> (K + 1)$-th” and subtract it from (F.1).
Then, we have to count the number of $(A _ 0, \dots, A _ {N - 1})$ for all $0 \leq x \leq R$ with $K$-th $= x$ and $(K + 1)$-th $< x$. But it is not countable directly. So we use a trick as follows:
\[
\begin{align}
& \left\{ \begin{aligned} K\text{-th} &= x, \\ (K+1)\text{-th} &< x, \end{aligned} \right. \\
= &
\left\{ \begin{aligned} K\text{-th} &\geq x, \\ (K+1)\text{-th} &< x, \end{aligned} \right.
-
\left\{ \begin{aligned} K\text{-th} &\geq x + 1, \\ (K+1)\text{-th} &< x, \end{aligned} \right. \\
= &
\left\{ \begin{aligned} K\text{-th} &\geq x, \\ (K+1)\text{-th} &< x, \\ A _ 0 + \dots + A _ {N - 1} &\leq R, \end{aligned} \right.
-
\left\{ \begin{aligned} K\text{-th} &\geq x, \\ (K+1)\text{-th} &< x, \\ A _ 0 + \dots + A _ {N - 1} &\leq R - K. \end{aligned} \right.
\end{align}
\]
Therefore, if we solve following problem, we can compute the final answer.
Problem F.1: Let $N, K \in \mathbb{N}$ with $K \leq N$. Let $x, R \in \mathbb{N} _ +$. Count the number of tuples $A = (A _ 0, \dots, A _ {N - 1}) \in \mathbb{N} ^ N$ which satisfies the following conditions. \[ \left\{ \begin{aligned} K\text{-th} &\geq x, \\ (K+1)\text{-th} &< x, \\ A _ 0 + \dots + A _ {N - 1} &\leq R. \end{aligned} \right. \]
Inclusion-exclusion principle
We can compute the answer of Problem F.1 by deep understanding of inclusion-exclusion principle. Fix $N$, $K$, $R$, and $x$. We write
$a _ k = $ the answer of Problem F.1 when $K = k$.
First, we choose $k$ elements in $N$. Without the lack of generality, we can assume $A _ 0, \dots, A _ {k - 1} \geq x$ and $A _ k + \dots + A _ {N - 1}$. This means that we may count tuples with $A _ 0, \dots, A _ {N - 1} \geq 0$ and $A _ 0 + \dots + A _ {N - 1} \leq R - kx$. We use $s _ k$ to denote this number of count, i.e.,
\[
s _ k = \begin{pmatrix} N \\\ k \end{pmatrix} \begin{pmatrix} R - k x + N \\\ N \end{pmatrix}. \tag{F.2}
\]
Unfortunately, this is not equal to $a _ k$. That’s because it also includes $a _ {k + 1}, \dots, a _ N$. How many times $a _ l$ is counted for $l = k, k + 1, \dots, N$? We’ve counted the number of tuples with $A _ 0, \dots, A _ {N - 1} \geq 0$ and the constraint of the sum. Just choose $k$ elements in $l$ and that is the coefficient. Then, we have
\[
s _ k = \sum _ {l = 0} ^ N \begin{pmatrix} l \\\ k \end{pmatrix} a _ l. \tag{F.3}
\]
We use a matrix to illustrate (F.3). We define
\[
S = \begin{pmatrix} s _ 0 \\\ \dots \\\ s _ N \end{pmatrix},
A = \begin{pmatrix} a _ 0 \\\ \dots \\\ a _ N \end{pmatrix} \in \mathbb{N}^{N + 1},
\]
and $X = (x _ {ij}) \in M _ {N + 1} (\mathbb{N})$ with
\[
x _ {ij} = \begin{pmatrix} j \\\ i \end{pmatrix}.
\]
Then (F.3) means $S = XA$. We use $Y$ to denote the inverse of $X$, i.e., $Y = (y _ {ij}) \in M _ {N + 1} (\mathbb{N})$ with
\[
y _ {ij} = (-1)^{i + j} \begin{pmatrix} j \\\ i \end{pmatrix}.
\]
Therefore, with (F.2), we conclude that
\[
\begin{align}
a _ K &= \sum _ {l = 0} ^ N (-1) ^ {l + K} \begin{pmatrix} l \\\ K \end{pmatrix} s _ l \\
&= \sum _ {l = 0} ^ N (-1)^{l + K} \begin{pmatrix} l \\\ K \end{pmatrix} \begin{pmatrix} N \\\ l \end{pmatrix} \begin{pmatrix} R - lx + N \\\ N \end{pmatrix}. \tag{F.4}
\end{align}
\]
Here, we note that the out-of-range combination numbers mean $0$.
Time-complexity
To calculate (F.4), $l$ will need to run only under the condition $K \leq l \leq N$ and $N \leq R - lx + N$, which means the time-complexity will be estimated as $O(R/x)$. Thus to calculate the sum of $0 \leq x \leq R$, we spend $O(R \log R)$-time. And this point will be the critical point of time-complexity.
