AtCoder Grand Contest 037
Updated:
Source codes
Solutions
A - Dividing a String
模範解答
貪欲法でやっても解けるが、末尾の処理が難しいので DP で解くことにする。そのためにまず次の補題を示す。
補題 A.1:最長の分割においては、長さ $5$ 以上の部分文字列は存在しない。
証明:長さ $5$ 以上のところは、必ずさらに分割が可能であることを示す。分割の仕方は $(1, 4)$, $(2, 3)$, $(3, 2)$,$(4, 1)$ のいずれかがありうる。そもそも文字数が違うので、分割後の $2$ つの文字列が一致することはない。したがってその両隣の文字列と一致する可能性だけ考慮すればいいが、それで潰れるのはせいぜい $2$ 通りだけなので、必ず $2$ 通り以上は生き残る。これは最長の分割であるという仮定に反する。これが示すべきことであった。
よって DP で $O(N)$ で解ける。次の DP では $j = 1, 2, 3, 4$ である。
$DP[i][j] = i$ 文字目までみて、最後の文字列が $S[i - j, i)$ である場合の最長の文字列の分割の仕方。
その必要はないのだが、 $S$ の冒頭に 'X' を追加して、これを番兵とする。 $N = \lvert S \rvert$ とする。初期状態: $DP[1][1] = 0$, otherwise $0$. 答え: $\max _ j DP[N][j]$. 遷移: $i = 1, \dots, N - 1$ に対し、 $j = 1, \dots, 4$ に対し、 $k = 1, \dots, 4$ に対し、 $S[i - j, i) \neq S[i, i + k)$ ならば、
\[
DP[i + k][k] \gets \max(DP[i + k][k], DP[i][j] + 1).
\]
ただし範囲外参照の場合は continue; する。
ポイント
これを DP で解くのが上級者か…と思った。
B - RGB Balls
コストの言い換え
この問題のコスト $c _ i - a _ i$ をまず言い換える。文字列の上を、文字列をカードの上に管理した人が歩いていくものとする。 $RGB$ の組が完成したら文字列を消去することにする。例えば $S = ``RRRGGGBBB”$ の場合は
\[
\begin{align}
C _ 0 &= \emptyset, C _ 1 = \{ R \}, C _ 2 = \{ R, R \}, C _ 3 = \{ R, R, R \}, \\
C _ 4 &= \{ RG, R, R \}, C _ 5 = \{ RG, RG, R \}, C _ 6 = \{ RG, RG, RG \}, \\
C _ 7 &= \{ RG, RG \}, C _ 8 = \{ RG \}, C _ 9 = \emptyset.
\end{align}
\]
となる。すると完成した各文字列について、 コストは文字列に生存期間に等しい 。すなわちコストの和は
\[
\sum _ {i = 0} ^ {3N} \sharp C _ i
\]
に等しい。したがってこの数字を最小にすることが、我々の仕事である。
解答
すると、操作が、ある一定の自由度をのぞいてほぼ一意に定まってしまうことがわかる。
わかりやすいように今まででできた文字列について $\sharp R \leq \sharp G \leq \sharp B$ を仮定する。すると今まで $\sharp R$ 個を完成させているのが最善である。カードには $GB$ が $\sharp G - \sharp R$ 個書かれていて(管理上 $GB$ と $BG$ は区別する必要はない)、 $B$ が $\sharp B - \sharp R$ 個書かれているのが最善であることもわかる。ここに $R$ が飛び込んでくると $GB$ と結合させて生存させないようにするのが最善である。 $G$ が飛び込んでくると $B$ とくっつけるのが最善である。 $B$ が飛び込んでくると新しく $B$ を作るしかない。よって消し方、くっつけ方に自由度があるので、それを掛け算すると答えになる。
ただし最後に人に文字列を配るために $N!$ をかける必要はある。
ポイント
これは生存期間の言い換えができなくて解けなかった。
C - Numbers on a Circle
解答
$\{ B _ i \}$ に対し操作を逆にし $\{ A _ i \}$ にすることを考える。まず $B _ i > B _ {i - 1} + B _ {i + 1}$ となっている所にしか操作ができない。この場合に重要なのが、 $B _ {i - 1}$ と $B _ {i + 1}$ については 操作ができない という事実である。 $B _ i$ が大きすぎて、それらについては操作することはできない。
したがって、操作が可能である数字は、必ず $1$ 個以上飛ばして待機しているはずである。ゆえに、これらの操作の順序は最終結果には影響しないとわかる。よって操作が可能な場所は局所的に判定できるが、操作をして問題がないとわかる。
ここで操作の回数は $B _ i / (B _ {i - 1} + B _ {i + 1})$ 回であり、操作後の数字は $B _ i \% (B _ {i - 1} + B _ {i + 1})$ である。ただし $A _ i$ 未満になってはいけない。その場合はストップする必要がある。ストップしない場合に限り、次に操作が可能になる数字は $B _ {i - 1}, B _ {i + 1}$ のいずれかである。
実装
以上の操作の部分を実装すると以下のようになる。
void update(int v)
{
int before = (v + N - 1) % N;
int after = (v + 1) % N;
ll a_c{B[before] + B[after]};
ll cnt{B[v] / a_c};
ll mod{B[v] % a_c};
if (cnt == 0)
{
return;
}
if (mod >= A[v]) // この場合はストップしない。
{
B[v] = mod;
ans += cnt;
B_sum -= a_c * cnt;
Q.push(before); // 隣の数字が次の候補になる。
Q.push(after);
}
else
{
if ((A[v] - mod) % a_c == 0)
{
B[v] = A[v];
cnt -= (A[v] - mod) / a_c; // 操作しすぎた分を戻す。
ans += cnt;
B_sum -= a_c * cnt;
}
else
{
No();
}
}
}
操作は、一致する可能性が出てくるところまでやる。
void solve()
{
while (A_sum < B_sum && !Q.empty())
{
update(Q.front());
Q.pop();
}
if (A_sum == B_sum)
{
same(); // 一致判定。
}
else
{
No();
}
}
queue<int> Q; で十分である。初期状態は全部放り込んでおけばいい。
計算量について
それぞれの頂点が何回 update されるかを考察する。すると update 後は 最低でも $B[i]$ は半分になっている (かまたはストップしてそれ以上触らない)のだから、 $\log _ 2 B[i]$ 回しか操作しない。つまり $M = \max _ i B _ i$ とすると、計算量は $O(N \log M)$ で抑えられる。
ポイント
これは普通にやった。計算量の見積もりだけが自信がなかった。
D - Sorting a Grid
Assume $0$-indexed.
Solution
We work on the transition $A \to B \to C \to F$, where $F$ is the final state. We see that $C \to F$ is just sorting each line. So we can hereby consider $A[i][j]$ as $A[i][j] / M$ and there are $M$ elements whose ID is $0, \dots, N - 1$. We also see that $B \to C$ is just sorting each column. Thus what we have to do is determine how to convert $A$ into $B$ so that each column has exactly one element for each $0, \dots, N - 1$.
We can do this by bipartite graph matching. We construct the following bipartite graph.
- The nodes $i = 0, \dots, N - 1$ denote the line numbers of $A$.
- The nodes $j = N, \dots, 2N - 1$ denote the line numbers of $B$.
- An edge between $i$ and $j$ with ID $a$ denotes that $a$ is put on the line $i$ on $A$ and should go on the line $j$ on $B$, i.e., $a = A[i][x]$ and $a / M = j$.
Here we can find perfect matchings $M$ times. For each time, we mark the edges we have used to make that matching as we used, and we no longer use it to make another matching.
The following picture explains how to construct the solution on the sample input 3.
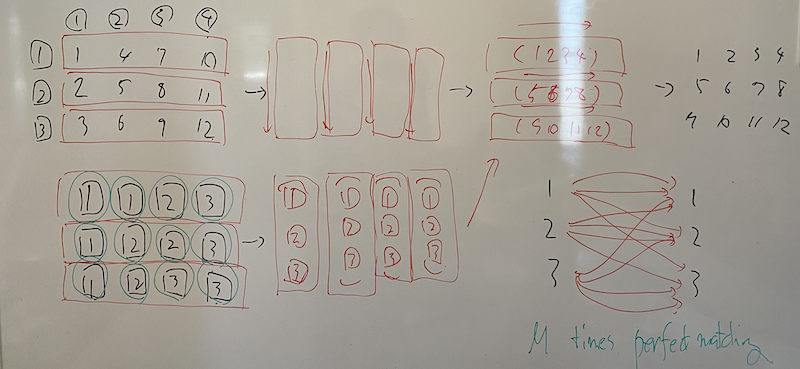
Proof of the solution
Showing the following proposition is suffice.
Proposition D.1: Let $G = (2N, E)$ be an bipartite graph composed of a pair of $N$ nodes. Suppose that each node’s degree is $M$. Then, there exist a perfect matching.
Proof: We use the maximum-flow-minimum-cut theorem. We use $S$ to denote the source and $T$ to denote the destination. It is suffice to show that every cut has at least the capacity $N$. Assume to the contrary that there exist a cut whose capacity is less than $N$. Every path from $S$ to $T$ is presented as $S \to x \to y \to T$ and it has been cut now. Each edge has the capacity $1$, so without loss of generality, there is no removed edge between $N$ and another $N$. Suppose that we have cut $X$ edges of $S \to x$ and $Y$ of $y \to T$. The fact that the capacity of cut is less than $N$ means that $X + Y < N$. We use $X, Y$ to denote its nodes, too. Now $G$ is cut, so between $x$-side and $y$-side, there are three types of edges on $G$.
- $x \in X$ and $y \in Y$,
- $x \in X$ and $y \not \in Y$,
- $x \not \in X$ and $y \in Y$.
Here we count the number of the edge in $G$. This is at most $M \lvert X \cup Y \lvert$, which is less than the actual number $MN$. This is a contradiction. So we admit that every cut has at least the capacity $N$, which completes the proof.
E - Reversing and Concatenating
Observation
Our final result will be a string whose length is $N$. If it is aaa...aaa, it must be lexicographically smallest. If we have a a in $S$, we can obtain a resulting string starting a.... So our first aim is to determine the smallest character in $S$. Without loss of generality, we can assume it is a.
The next aim is to determine how long we can continue a by starting position. Let $U$ be the concat of $S$ and the reverse of $S$. If $K = 1$, we have $N + 1$ possibilities and just trying them all is suffice. So hereinafter assume $K \geq 2$. The next proposition is a clue to solve this problem.
Proposition E.1: Let $L$ be the maximum length of ascending
as. Then, the minimum resulting string starts $2 ^ {K - 1} L$as.
Proof: We can construct resulting string starting with $2 ^ {K - 1} L$ as by a greedy algorithm. For $i = 0, \dots, K - 2$, The $i$-th manipulation should be to choose a string which ends by $2 ^ {i - 1} L$ as as $S$. Then, the next $U$ has $2 ^ i L$ ascending as. So the mathematical induction works here. The $K - 1$-th manipulation is to cut out $S$ starting by $2 ^ {K - 1} L$ as.
To the contrary, we cannot go further. For any $S$ with a $X$ ascending as, $U$ has at most $2X$ ascending as. Thus we cannot have $2^{K - 1} L$ as through $K$ manipulations.
In addition, we care for the fact that except the first manipulation, we have one way to gain the resulting string starting $2 ^ {K - 1} L$ as. So we try all of the $N + 1$ candidates.
Solution
First, determine the smallest character in $S$. We write it as a. Second, construct the initial $U$ and determine $L$. We try $N + 1$ candidates. If $K = 1$, the answer is the smallest one. If $K \geq 2$, the resulting string can be start by $2 ^ {K - 1} L$ as. Thus if $N \leq 2 ^ {K - 1} L$, the answer is aaa...aaa.
Otherwise we try the $N + 1$ candidates. Each of them are simulated in exactly one way and each of them can be manipulated in $O(NK)$-time. The answer is the minimum. Note that in this case we have $K = O(\log N)$. Therefore the total time complexity will be $O(N^2 \log N)$.
F - Counting of Subarrays
We are given a fixed $L \geq 2$. So we simply call level $(K, L)$ as level $K$.
Observation
We are going to count the number of valid ranges in ascending order of level $K$. Suppose there is an element whose number is $1$. We start by $K = 1$.
Example 1
To explain the observation, we use the following example with $L = 3$. \[ 2, 1, 1, 1, 1, 1, 1, 2, 3. \] Of course we are working on the continuous $1$s. \[ 2, (1, 1, 1, 1, 1, 1), 2, 3. \] We see there is $15$ level-$1$ ranges here. After considering the level-$1$ ranges, we regard $(1, 1, 1, 1, 1, 1)$ as $(2, 2)$. Thus here we count the level-$2$ ranges of \[ (2, [2, 2], 2), 3. \] We will work the same thing on $(2, 2, 2, 2)$ to see $3$ level-$2$ ranges. Then, pressing $(2, 2, 2, 2)$ into $3$ to have \[ ([3], 3). \] There is no level-$3$ range. Pressing $(3, 3)$ result in “empty” $4$. The observation is terminated.
What’s the answer? Don’t forget the single number $x$ is a level-$x$ range. The answer is \[ N + 10 + 3 = 22. \]
Example 2
Let’s consider the second example with $L = 2$.
\[
2, (1, 1, 1, 1, 1, 1), 2, 3.
\]
We see $15$ level-$1$ ranges. We press $(1, 1, 1, 1, 1, 1)$ into $(2, 2, 2)$ to have
\[
(2, [2, 2, 2], 2), 3. \tag{F.1}
\]
There is several choice to choose the mid $[2, 2, 2]$. But they are originally consist of $1$s. Thus, for example, taking the first two $2$s, there is several possibility.
\[
\begin{align}
& 2, 1, 1, \\
& 2, 1, 1, 1.
\end{align} \tag{F.2}
\]
How can we manage to overcome this problem? Notice that this problem is a kind of DP. When we pressed $(1, 1, 1, 1, 1, 1)$ into $(2, 2, 2)$, we regard the first two $1$s and three $1$s are the same to think of (F.2). But the situation is not so simple. Consider the third or fourth $2$s. There is two possibility as follows.
\[
\begin{align}
& 1, (1, 1, 1, 1, 1), \\
& 1, 1, (1, 1, 1, 1).
\end{align}
\]
The first two ones are divided the above way. So we have to distinguish the first $1$ and the second $1$. In addition, we don’t distinguish $([1, 1], [1, 1, 1])$ and $([1, 1, 1], [1, 1])$.
Therefore, we come up with an idea that we also have $L _ i$ and $R _ i$ with pressed element.
The idea is as follows. First, we initialize all $L _ i = 1$ and all $R _ i = 1$. To count level-$1$ ranges, we have
\[
\begin{align}
A &= \{ 2, (1, 1, 1, 1, 1, 1), 2, 3 \}, \\
L &= \{ 1, (1, 1, 1, 1, 1, 1), 1, 1 \}, \\
R &= \{ 1, (1, 1, 1, 1, 1, 1), 1, 1 \}.
\end{align}
\]
So we can count the number of level-$1$ ranges by
\[
L _ 1 (R _ 2 + \dots + R _ 6) + L _ 2 (R _ 3 + \dots + R _ 6) + \dots + L _ 5 R _ 6 = 15.
\]
When we press $(1, 1, 1, 1, 1, 1)$ into $(2, 2, 2)$, we also press $L$ and $R$.
\[
\begin{align}
A &= \{ (2, [2, 2, 2], 2), 3 \}, \\
L &= \{ (1, [1, 2, 2], 1), 1 \}, \\
R &= \{ (1, [2, 2, 1], 1), 1 \}.
\end{align}
\]
But here, we have to subtract the answer by the level-$2$ ranges completely consisting of $[2, 2, 2]$. It has been counted as level-$1$ ranges. Note that we count the number of ranges, regardless its level. We have to subtract
\[
L _ 1 (R _ 2 + R _ 3) + L _ 2 R _ 3 = 3 + 2 = 5.
\]
Then, we can count the number of level-$2$ ranges by
\[
L _ 0 (R _ 1 + \dots + R _ 4) + L _ 1 (R _ 2 + \dots + R _ 4) + \dots + L _ 3 R _ 4 = 6 + 4 + 4 + 2 = 16.
\]
We press $(2, 2, 2, 2, 2)$ into $(3, 3)$ to have
\[
\begin{align}
A &= \{ ([3, 3], 3) \}, \\
L &= \{ ([2, 4], 2) \}, \\
R &= \{ ([4, 2], 1) \}.
\end{align}
\]
We have to subtract
\[
L _ 0 R _ 1 = 4.
\]
Then, we can count the number of level-$3$ ranges by
\[
L _ 0 (R _ 1 + R _ 2) + L _ 1 R _ 2 = 6 + 4 = 10.
\]
The final pressing result in a $4$, which does not regarded as level-$4$. The answer is
\[
N + 15 - 5 + 16 - 4 + 10 = 41.
\]
Example 3
Now we have all the keys except a corner case to solve this problem. But to understand deeply, we work another example with $L = 3$.
\[
\begin{align}
A &= \{ 4, 3, 2, (1, 1, 1), 2, 3, 2, 2, (1, 1, 1), 2, 2 \}, \\
L &= \{ 1, 1, 1, (1, 1, 1), 1, 1, 1, 1, (1, 1, 1), 1, 1 \}, \\
R &= \{ 1, 1, 1, (1, 1, 1), 1, 1, 1, 1, (1, 1, 1), 1, 1 \}.
\end{align}
\]
We find $2$ level-$1$ ranges. We press them to have
\[
\begin{align}
A &= \{ 4, 3, (2, 2, 2), 3, (2, 2, 2, 2, 2) \}, \\
L &= \{ 1, 1, (1, 1, 1), 1, (1, 1, 1, 1, 1) \}, \\
R &= \{ 1, 1, (1, 1, 1), 1, (1, 1, 1, 1, 1) \}.
\end{align}
\]
We find $7$ level-$2$ ranges. We press them to have
\[
\begin{align}
A &= \{ 4, (3, 3, 3, 3) \}, \\
L &= \{ 1, (1, 1, 1, 3) \}, \\
R &= \{ 1, (1, 1, 1, 3) \}.
\end{align}
\]
We find $7$ level-$3$ ranges. We press them to have
\[
\begin{align}
A &= \{ (4, 4) \}, \\
L &= \{ (1, 2) \}, \\
R &= \{ (1, 4) \}.
\end{align}
\]
We find $0$ level-$4$ ranges. We press them to have
\[
\begin{align}
A &= \{ \emptyset \}, \\
L &= \{ 0 \}, \\
R &= \{ 0 \}.
\end{align}
\]
We stop here to calculate the answer, which is added up to
\[
N + 2 + 7 + 7 = 31.
\]
Corner case
Suppose we are given the following $A$ with $L = 4$. \[ A = \{ 100, 100, 1, 100, 100 \}. \] The answer is $0$, but if we mistakenly press $1$ into empty, it will become \[ A = \{ 100, 100, 100, 100 \}. \] We will mistakenly find a level-$100$ range. To prevent this type of mistake, we should insert $\emptyset$ to have \[ A = \{ 100, 100, \emptyset, 100, 100 \}. \]
Implementation
Estimate of time-complexity
The idea of the solution has been presented above. But in order to reduce time-complexity, we need a good plan.
What will be the lower bound of the order of the time complexity of the algorithm argued above? The answer is $\Omega(N \log N)$.
This is because when we press $X$ element by one manipulation, we delete $X$ elements and then add $X / L \leq X / 2$ elements as unmarked. So the entire length of $A$ will shrink, but we have to touch them. The total number of the touch of the elements will be $\Omega(N \log N)$.
What we have to care is that we cannot touch the entire $A$ in a single manipulation; otherwise we will spend $O(N^2)$-time. Suppose we work on level-$K$ ranges. We must not touch the elements whose number is not $K$. How can we do that?
How to hold $A$
We can solve this problem by using std::set. First, we define a class Element as follows.
struct Element
{
int ind;
ll left, right;
boost::optional<int> value; // for C++14
bool operator<(Element const &rhs) const
{
return ind < rhs.ind;
}
bool operator==(Element const &rhs) const
{
return ind == rhs.ind;
}
};
We use boost::optional<int> value; to denote the value of the element with $\emptyset$ being boost::none. When AtCoder allows us to use C++17, it will be std::optional<int> and std::nullopt.
We define $A$ by set<Element> A;. To compare two elements, we compare their index.
Helper indexes
We implement the code as an entire class Solve as follows.
class Solve
{
int N, L;
set<Element> A;
map<int, vector<int>> indexes; // value -> inds
public:
Solve(int N, int L, vector<int> input) : N{N}, L{L}
{
for (auto i = 0; i < N; i++)
{
A.insert({i, 1, 1, input[i]});
indexes[input[i]];
indexes[input[i]].push_back(i);
}
}
ll count(); // return answer, working each level.
private:
void update(ll &ans, vector<Element> &tmp);
{
ans += calc(tmp);
tmp = press(tmp);
ans -= calc(tmp);
for (auto e : tmp)
{
A.insert(e);
}
tmp.clear();
}
ll calc(vector<Element> const &X); // calculate for the number of range
vector<Element> press(vector<Element> const &V); // return the pressed (value + 1)-valued elements
The most important point here is that we use a helper map indexes. This holds the elements’ values as keys, and its indexes by vector<int>. By using indexes, we don’t have to touch by each level.
How to determine whether the adjacent has the same value
ll Solve::count()
{
ll ans{N};
while (!indexes.empty())
{
vector<Element> tmp;
auto &vec{indexes.begin()->second};
sort(vec.begin(), vec.end());
int min_value{indexes.begin()->first};
for (auto ind : vec) // in order not to touch all elements of A.
{
auto it{A.find(make_element(ind))};
assert(it != A.end()); // it must be found.
tmp.push_back(*it);
it = A.erase(it); // We must erase elements before inserting pressed elements. Fortunately `erase` returns the next iterator.
if (it == A.end() || it->value != min_value)
{
update(ans, tmp);
}
}
if (!tmp.empty())
{
update(ans, tmp);
}
indexes.erase(indexes.begin());
}
return ans;
}
Thanks to indexes, we directly access the level-$K$ elements. Remember that we have $A$ by set<Element>. So we can determine whether the adjacent has the same value or not by its iterator. The most important point here is that we have to maintain relative order of indexes, but don’t have to care about its adjacent because it can be determine by its iterator. So by computing vector<Element> press(vector<Element> const &V), we just keep its relative order of both entire $A$ and its local pressed range.
Time complexity
The resulting time complexity is $O(N \log ^ 2 N)$.
