AtCoder Beginner Contest 131
Updated:
Source codes
Solutions
A - Security
文字列 $S$ で持っておき $i = 0, 1, 2$ に対し $S[i] = S[i + 1]$ が $1$ 個でも見つかれば Bad, そうでなければ Good とする。
B - Bite Eating
解説放送の模範解答 $O(N^2)$
言われた通りにやればいい。
模範解答 $O(1)$
全部の和を $S$ とする。全部から $a _ i = L + i - 1$ の美味しさのりんごを除いたものの和を $T$ とする。すると $\lvert S - T \rvert = \lvert a _ i \rvert$ である。よって $\lvert a _ i \rvert$ が最小のもの $X$ を $S$ から引けばいい。
\[
S = \sum _ {i = 1} ^ N (L + i - 1) = N(L - 1) + \frac{N(N + 1)}{2}
\]
である。さらに
\[
X = \begin{cases}
L + N - 1 & L + N - 1 \leq 0, \\
L & L \geq 0, \\
0 & \text{otherwise}.
\end{cases}
\]
である。これで $O(1)$ で答えられる。
ポイント
$O(N^2)$ で解いた。
C - Anti-Division
$f(x) = [1, x]$ で条件を充たす場合の数
とすると、答えは $f(B) - f(A - 1)$ である。包除原理により \[ f(x) = x - x / C - x / D + x / \text{lcm}(C, D). \] ただし割り算は計算機の割り算。ここで $\text{lcm}(C, D) = CD / \text{gcd}(C, D)$ である。
ポイント
$[0, x)$ でやったので少し違ったがほぼ同じ解法である。
D - Megalomania
解答
$\{ (A _ i, B _ i) \}$ を $B _ i$ が小さい順にソートする。その順に仕事をやってみて締め切りに間に合うなら Yes, そうでないなら No である。
解答の正当化
次の定理を示せば良い。
定理: この問題の答えが
Yesであるならば、 $\{ (A _ i, B _ i) \}$ を $B _ i$ の小さい順に並べたものが実際に完遂できる。
証明: $0$-indexed とする。 $\{ (A _ i, B _ i) \}$ をやる順番で並べたとする。これが Yes であると仮定する。仮に $i \in N - 1$ が存在して $B _ i > B _ {i + 1}$ が成立していると仮定する。 $S = \sum _ {j = 0} ^ {i - 1} A _ j$ とする。仮定により $S + A _ i \leq B _ i$ かつ $S + A _ i + A _ {i + 1} \leq B _ {i + 1}$ である。すると後者より
\[
S + A _ i + A _{i + 1} \leq B _ {i + 1} < B _ i.
\]
さらに
\[
S + A _ {i + 1} < S + A _ i + A _ {i + 1} \leq B _ {i + 1}.
\]
よって $i$ と $i + 1$ を入れ替えても仕事が完遂できることになる。
E - Friendships
解答
まず $K$ の下限は $0$ である。完全グラフがこれを充たす。
$K$ の上限は star で達成される。 $(N - 1)(N - 2) / 2$ である。その理由:まず頂点の組の数は $N (N - 1) / 2$ である。これが連結がグラフになるためには辺が $N - 1$ 本必要である。それで結ばれる組の最短経路は $1$ である。よってそれらはカウントされえない。以上より、次式が得られる。 \[ K \leq \frac{N (N - 1)}{2} - (N - 1) = \frac{(N - 1)(N - 2)}{2}. \] この上界は star で達成される。
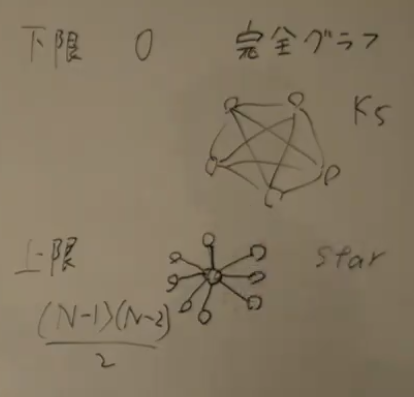
そしてこの上限と下限の間の $K$ は全て構築できる。 star の足となった頂点同士を繋ぐと、その間の距離は $2 \to 1$ になる。その他の組は $2$ から変化がない。よって距離 $2$ の点の組の個数が $1$ だけ減る。これを繰り返すと任意の $K$ が達成される。全て繋ぐと完全グラフになる。
実装
可能不可能判定のあと、素朴に辺を追加していけばよろしい。私はミスがないように無向グラフを普通に構築した。
F - Must Be Rectangular!
解答
$C = 10^5 + 5$ とする。
$x$ 座標を表す点 $0, 1, \dots, 10^5$ と $y$ 座標を表す点 $C, C + 1, \dots, C + 10^5$ を用意する。そして座標の点 $(x, y)$ を $x$ と $C + y$ を結ぶ 辺 であるとみなす。このグラフを $V$ とする。
この時、まずこれは自然な二部グラフである。操作は、長さ $3$ の(異なる頂点からなる) path があったら、その始点と終点の辺を張るということである。これをできるだけ繰り返した場合、最終形 $V’$ はどうなるかというと、次が成立する。
定理: $V’$ は、 $V$ の連結成分ごとの完全な二部グラフの union である。
証明:まず操作規則より、 $V$ の異なる連結成分の間に辺が張られることはない。そこで $V$ のある連結成分 $W$ を考える。 $W$ は $x, y$ 座標の区切りで二部グラフになっているが、任意の $x$ 側から $a$, $y$ 側から $b$ を選んでくる。 $(a, b) \not \in W$ と仮定する。連結性より、 $a$ と $b$ の間には $3$ 以上の奇数長の path がある。この path に上記の操作を順番に適用すると、長さの $1/2$ の回数(計算機の割り算)だけ辺を張る・またはすでに張られているのを確認する動作を繰り返すと、最終的に $(a, b)$ に辺が張られる。 $a, b$ の任意性により、 $W$ は最終的には完全な二部グラフへ操作される。
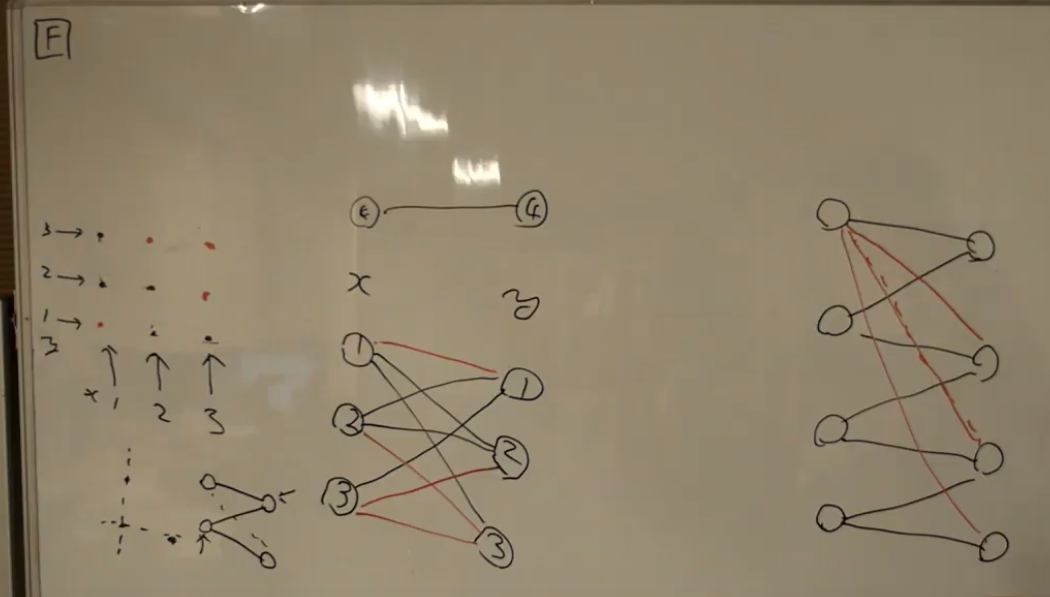
操作の回数は、以下で求まる。 \[ \left( \sum _ {W \subset V} \lvert W _ x \rvert \lvert W _ y \rvert \right) - N. \] ここで $W \subset V$ は連結成分の走査であり、 $W _ x, W _ y$ はそれぞれ $W$ の $x$ 座標側、 $W$ の $y$ 座標側の頂点の集合である。 $\lvert \cdot \rvert$ は頂点の個数を表している。
実装
要するに $W$ は dfs で求めることができる。 $\lvert W _ x \rvert$, $\lvert W _ y \rvert$ をカウントしていき、和に突っ込む。最後に $N$ を引けば良い。
ポイント
本番では Union-Find でやったけど、これは snuke さんの解法の方が素朴で綺麗だと思った。
$2$ 次元座標の点を $x$ 座標から $y$ 座標への辺だとみなす のは定跡である。
Others
A - sample: 4, tle: 2.000, time: 02:11, from_submit: 63:50
B - sample: 3, tle: 2.000, time: 08:40, from_submit: 55:10
C - sample: 3, tle: 2.000, time: 04:19, from_submit: 50:51
D - sample: 3, tle: 2.000, time: 03:42, from_submit: 47:09
E - sample: 2, tle: 2.000, time: 11:36, from_submit: 35:33
F - sample: 3, tle: 2.000, time: 35:33, from_submit: 00:00
