AtCoder Regular Contest 100
Updated:
Source codes
beta 版で自動提出機が動いたので満足。
E まで完成。
Solutions
C - Linear Approximation
$0$-indexed とする。 $B_i = A_i - i$ として、 $\sum_{0 \leq i < N} \lvert B_i - b \rvert$ を最小化すれば良い。ソートすることで ${ B_i }$ は単調増加として良い。 $b$ は中央値、すなわち $b = B_{N/2}$ とすると最小値が得られる。
最小値が得られることの正当化
$x \to \pm \infty$ で求める値は $\infty$ になる。よって実際に $x$ が動く範囲はある有界集合上に限って良い。したがって最小値が存在する。
今立っている場所が最適解を与えていると仮定する。右に $M_1$ 個の点、左に $M_2$ 個の点があるとする。この時右に $\epsilon > 0$ だけ動くとする。すると求める値は $M_2 \epsilon - M_1 \epsilon$ だけ増える。よってこの値は $0$ 以下でなければならない。左に $\epsilon > 0$ 動いても同様である。したがって $M_0 = M_1$ が従う。よって中央値で最小値が得られる。
D - Equal Cut
問題が仮に「 $2$ つの空でない連続する部分列に分解」である場合、両者の和の差を最小化するようにするのが最適である。これは imos 法で前処理 $O(N)$ しておくだけで二分探索で $O(\log N)$ でできる。 $\max(P, Q, R, S) = \max(\max(P, Q), \max(R, S))$ および $\min$ も類比的であることを考慮すると、結局 $(P, Q)$ と $(R, S)$ の境目を全探索で決めれば後は $O(\log N)$ で応答できる。計算量は $O(N + N \log N)$ である。実際は imos 法で $O(N)$ で解けるらしい。
ポイント
こうやって書けば簡単であるが、初手は間違えてしまった。 $P$ を全探索して、 $S$ を決めてから、 $(Q, R)$ を上の方法で決めるという方針にしてしまった。
割と早めにミスに気づけた。
E - Or Plus Max
コンテスト中に思いついた解法
まず、
$DP[i] = $ ( $K = i$ のときの答え)
とする。すると結局
$DP2[K] = $ (ぴったり $(i \lor j) = K$ を充たす $(i, j)$ について、 $A_i + A_j$ の最大値)
とすると、最小値の定義から、 \[ DP[i] = \max(DP2[i], DP[i-1]) \] と遷移するのがわかる。そこで高速に $DP2$ を求めることに帰着するが、ここで最終的に $\max$ を取るので、前ですでに $DP[i-1]$ に吸われていた項が $DP2$ に入っていても、答えは変わらない。そこで、 $DP2$ の定義を以下の通りに 変更 する。
$DP2[K] = $ ( $(i \lor j) \subset K$ を充たす $(i, j)$ についての $A_i + A_j$ の最大値)
ここで $a \subset b$ とは、「任意の $a$ の立っているビットについて $b$ も立っている」という意味である。すぐにわかる通り、集合 \[ S_K = \{ A_j \mid j \subset K \} \] の大きいものを順に $2$ つ取り出してその和を求めれば $DP2[K]$ になる。
そこでいかに高速に $S_K$ を求めるかが焦点である。結局全ての $1 \leq K \leq 2^K - 1$ について答えを求めるので、 $S_K$ を求めるプロセス自体は省略できない。だから正直に求めると $O({2^N}^2)$ の時間がかかる。しかし使うのは上位 $2$ 個だけなので、上位 $2$ 個だけ求める方針でいく。以下、 $A_j$ は $(A_j, j)$ のペアで管理することに注意されたい。まず、 \[ S_K = \left( \bigcup_{ j \subset K, j \neq K } S_j \right) \cup \{ A_K, A_0 \} \tag{1} \] である。前者は DP または再帰的に求められる。すぐにわかる通り、 $K_1 \subset K_2$ に対して $S_{K_1} \subset S_{K_2}$ である。ゆえに $j$ として考えれば良いものは「 $K$ の立っているある $1$ つのビットを折ったもの」だけである。よって最大でも $N$ 個である。そして $\bigcup$ を愚直に取るのではなく、先ほど書いた通り上位 $2$ 個だけ取ってマージする。よって操作する元の数は $2 N + 2$ 個を超えない。
以上により、計算量は $O( 2^N \cdot N \log N + 2^N)$ である。これは間に合う。
ポイント
間違えた箇所は以下の通り。
(1 << N)にするべき箇所をNにしてしまった。- RE を出した。 $N \leq 18$ であるから $200010 < 2^{18} < 300010$ である。
高速ゼータ変換
この問題は (1) のところで高速ゼータ変換を使用するのが模範解答であるようだ。高速ゼータ変換について述べる。
例題
$X$ を集合とする。 $f \colon \mathcal{P}(X) \to \mathbb{N}$ とする。 $g \colon \mathcal{P}(X) \to \mathbb{N}$ を次式で定める。 \[ g(A) = \sum_{Y \subset A} f(A). \] このとき、すべての $A \subset X$ に対して $g(A)$ を求めよ。
注釈
この問題において $(\mathbb{N}, +)$ は 可換な半群 であればなんでもよろしい。例えば $(\mathbb{Z}, \max)$, $(\mathbb{N}, \mathrm{gcd})$ や、 $S$ を集合としたときに $(\mathcal{P}(S), \cup)$ でもよろしい。
例題の解答
DP をする。 $N = \lvert X \rvert$ とする。 $0 \leq n < N$, $A \subset X$ に対し、 $DP[n][A]$ を以下の通りに定める。 \[ DP[n][A] = \sum_{Y \subset A, Y[n, N) = A[n, N)} f(Y). \] ここで $Y[n, N) = A[n, N)$ は $2$ 進法表記での部分文字列として一致しているという意味である。すると、
- 答え: $g(A) = DP[N][A]$
- 初期状態: $DP[0][A] = f(A)$
は即座にわかる。あとは遷移である。任意の $1 \leq i \leq N$ に対し、任意の $j \in \mathcal{P}(X)$ に対し、
\[
DP[i][j] =
\begin{cases}
DP[i - 1][j] + DP[i][j \setminus \{ i - 1 \}] && (i - 1 \in j), \
DP[i - 1][j] && (i - 1 \not\in j)
\end{cases}
\]
である。計算量は $O(N \cdot 2^N)$ である。
具体例
$j = 100110100$ の場合を途中まで計算する。ワイルドカードを $X$ で表すことにする。
- $DP[0][100110100]$ は $100110100$ の総数である。つまり $f(100110100)$ である。
- $DP[1][100110100]$ は $100110100$ の総数である。つまり $DP[0][100110100]$ である。
- $DP[2][100110100]$ は $100110100$ の総数である。つまり $DP[1][100110100]$ である。
- $DP[3][100110100]$ は $100110X00$ の総数である。つまり $DP[2][100110100]$ に加えて、 $100110000$ の総数が欲しい。すなわち $DP[3][100110000]$ で求まる。
- $DP[4][100110100]$ は $100110X00$ の総数である。つまり $DP[3][100110100]$ である。
- $DP[5][100110100]$ は $1001X0X00$ の総数である。つまり $DP[4][100110100]$ に加えて、 $100100X00$ の総数が欲しい。すなわち $DP[5][100100100]$ で求まる。
解説放送での解説
bit が立っていないところに bit を立たせる DAG を作る。間のところが $DP[i][j]$ に相当する。緑色の線は $a_2 \in S_6$ を示している。
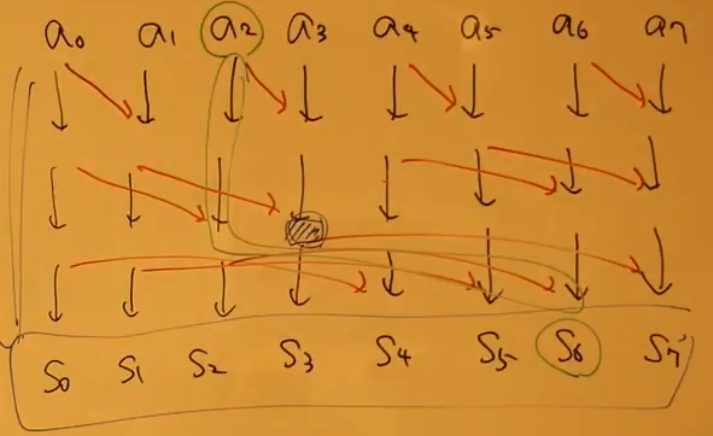
結局本問題はどうなるか
(1) は高速ゼータ変換で求めることができる形そのままである。ただし $\cup$ のマージが愚直にはできないので、上位 $2$ つだけをマージすればよろしい。上で述べた解法より優れていて計算量は $O( 2^N \cdot N + 2^N)$ に改善する。
私の解法で今回問題が解けたのは、 $\cup$ の場合は $+$ と違って重複が許されるからである。だから、高速ゼータ変換の方がよほど汎用性が高い。
参考文献
F - Colorful Sequences
ペンディング。以下はまだ解かれていません。
この問題は仮に カラフルの指定がなければ 簡単である。答えは $(N - M + 1) K^{N - M}$ である。そこでカラフルでない数列をすべて考えて、その中で $A$ が入っていない場合の数を求めてそれを引くことにする。以下この問題を解く。
$A$ をまずおいておく。次に $A$ の両端をカラフルでないように伸ばしていき長さ $N$ にするというプロセスで元の列を生成することにする。ここで自明なパターンとして、もし $A$ がすでにカラフルならばどう頑張ってもカラフルになるから答えは $0$ である。
準備
まず長さ $N$ のカラフルでない列は何通りあるのかを求める。これが準備運動。
$dp[i][j] = $ 長さ $i$ の数列で、カラフルでなく、さらにラスト $j$ 個は全て異なっており、かつ $j + 1$ 個は同じ要素を含むものの場合の数
とする。累積和を取ると $O(NK)$ になる。初期状態 $dp[0][0] = 1$ 。
以下場合分けをする。
- $A$ の要素で同じものがある。
- それ以外。つまり $A$ の要素が全部異なる。
同じものがある場合
全て異なる場合
ポイント
Others
惜しかった。後 10 分あれば E で AC 出たのだが。
C - sample: 4, tle: 2.000, time: 04:04, from_submit: 106:02
D - sample: 3, tle: 2.000, time: 38:22, from_submit: 67:39
E - sample: 3, tle: 2.000, time: 67:40, from_submit: 00:00
F - sample: 7, tle: 2.000, time: 00:00
