AtCoder Regular Contest 095
Updated:
GCJ Round 1 は体力温存のために諦め、 ARC だけやることにした。
解説全部書きました。
Source codes
Solutions
C - Many Medians
小さい方から見て $n/2 - 1$ 番目( $A$ とする)か $n/2$ 番目( $B$ とする)が答え。除く数字が $A$ 以下なら $B$ 、 それ以外は $A$ が答え。
D - Binomial Coefficients
$n$ はできるだけ大きく選び、 $k$ は $n/2$ にできるだけ小さいものを選ぶとよろしい。
ポイント
$n > k$ という不可解な制約があったので WA を取ってしまった。 $0 \leq k \leq n$ で良いのでは。 $k = 0$ を外すのはわからんでもないが、 $k = n$ を外すのは理解に苦しむ。
E - Symmetric Grid
全体の方針
基本的な考え方としては、丁寧に全探索することである。
まず最初に目が行くのは、この問題では入れ替えの具体的操作の出力を要求されていないことと、行の入れ替えと列の入れ替えは双方の順番は干渉しないということである。そこで、先に行の入れ替えをし、その後で列の入れ替えをすることにする。
小課題、列の全探索
ゆえに、行の入れ替えが行われた段階で、小課題として列の入れ替えだけで問題の条件を充たすことができるかどうかを解くことが最初のステップとなる。これは以下の動作でわかる: $0 \leq j < W$ に対し、行の入れ替えが済んだ後で上から下へ読んだ文字列 $V_1[j]$ と、下から上へ読んだ文字列 $V_2[j]$ を得る。 int cnt = 0; と vector<bool> used(W, false); を用意しておく。この後で $i = 0, \dots, W-1$ に対し、 !used[i] ならば、 !used[j] かつ $V_1[i] = V_2[j]$ となるような $i+1 \leq j < W$ を探し、見つかったら used[i] = used[j] = true; かつ cnt += 2; として break; しておく。ループが終わった段階で $W - \text{cnt} = 1$ ならば !used[i] となる $0 \leq i < W$ が存在するので、そいつについて $V_1[i] = V_2[i]$ ならば cnt++; する。この結果 $W = \text{cnt}$ ならば問題の条件を充たしている。そうでないならば、この行の入れ替えについては問題の条件を充たすことはできない。
行の全探索について
行の位置を $H!$ 通り全て試す必要はない。点対称になるかどうかは、相対的な位置、すなわちペアになる行がどれかで決まる。例えば $H = 3$ なら、
\[ ([0, 1], 2), ([0, 2], 1), ([1, 2], 0) \]
の $O(H!!)$ 通りしかない。だから vector<tuple<int, int>> 型でもっておけばよろしい($2$ は $[2, 2]$ とみなして差し支えない)。列挙は DFS でできる。
計算量
$O(H!! HW^2)$ だが、実際の $O(H!!)$ は $H$ が偶数なら $(H-1)!!$ である。 $11!! \approx 10^4$ 程度で、 $HW^2 \approx 10^3$ は文字列を作って比較するだけの十分軽い動作なので、 vector が少々遅くても、時間制限には間に合う。
ポイント
丁寧に全探索するだけなので、実装で間違えたところが重要である。今後ミスしないようにしたい。
- まず DFS で ペアにならないものは先に選んでおく 。先に選ばないせいで、正しく列挙できていなかった。
vector<bool> used = vector<bool>(W, false);のWとfalseを逆にしていた。vector<型>(個数, 値)である。- 列の全探索で、例外扱いになる $V_1[i] = V_2[i]$ の判定を間違えていた。 ペアになり得るものは貪欲にくっつけた方がいいので、自分をペアにするのは最終手段 である。だからループを抜けて最後に判定するとミスなく書ける。
発想としては、「行と列の入れ替えが独立な動作だから、行を固定して列の入れ替えを判定しよう」というように自然に小課題が思い浮かべばあとはストレートである。
F - Permutation Tree
まず、この能力で作れるグラフの形状を特定する。これにはいくつか試してみるといいが、問題文の設定だとやりにくくて仕方ない。こういう時は 置換は逆変換で捉える という定跡を考慮する。つまり $p_1, p_2, \dots$ ではなく $1, 2, \dots$ の順番で見ていくことにする。すると、この辺でつながるものは $p_i$ が小さい順から添字 $i$ に注目し次の手順でできるものである:
- 今まで触れてきた添字の集合 $I$ について $\max I$ と $i$ をつなぐ。ただし $I = \emptyset$ の時は何もしない。
- $I \gets I \cup \{ i \}$ とする。
これに気づくと、 $i$ とつなぐ点 $\max I$ は広義単調増加であることがわかる。そうすると、グラフの繋ぎ方は次のようになる。
- $\max I$ が変化しないとき、同じ点に枝が生える。
- 変化する時は、変化前の $\max I$ と変化後の $\max I$ がつながる。
その結果、グラフは以下の形状をしている。
- 単純な長さ $S$ の木がまずある(これを 胴体 と呼ぶ)。
- 胴体の点に長さ $1$ の枝がたくさんついている。
このグラフは キャタピラ と呼ばれるものだそうだ。胴体には最大長を仮定することにより、胴体の最初と最後の点には枝が生えていないとして良い。
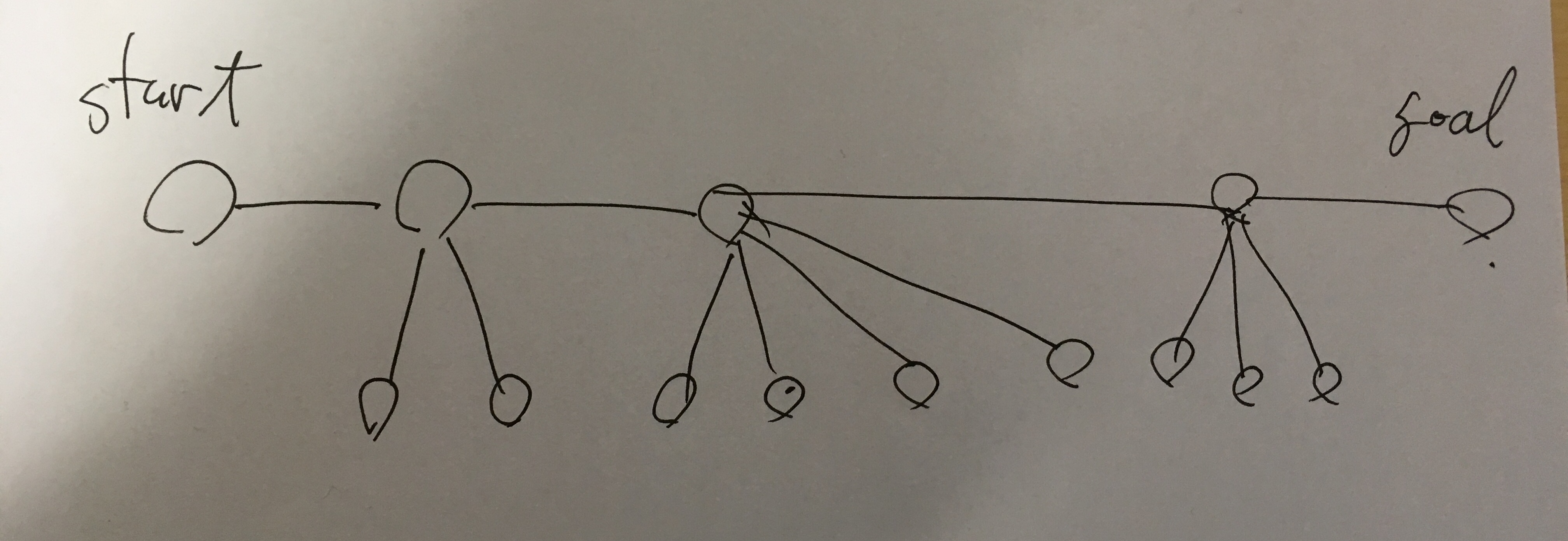
キャタピラは、胴体(の長さ)と、それらに生えている枝の数で形状が決定する。与えられたグラフがキャタピラかどうかは然るべき時に判断するとして、キャタピラだと仮定してまず胴体を決定しよう。これは直径を求めるだけでよろしい。足の長さが $1$ なので、全ての場合で直径を構成する点列と一致する。木の直径は「まず適当な点から最長の点を求める」「その点から最長の点を求める」で求まる。幅優先探索しておく。次に、直径を伝って胴体を構成する頂点を求める。これは幅優先探索してあるので、ゴールから $1$ 小さいところに戻るのを繰り返すだけでよろしい。
次にキャタピラ判定をすることにする。「胴体から直接出ていない辺が無い」ことを判定すればよろしい。これは簡単で、胴体から胴体以外の点へ伸びている辺の数の和を求め、その合計と胴体の頂点数の合計が $N$ になっているか判定する。
最後に、キャタピラを構成する辞書順最小の置換 $p$ を求める。手順 1., 2. が頭に入っていれば簡単である。胴体から $k$ 本生えている節を構成するには $(1, 2, \dots, k, 0)$ とすればよろしい。あとは番号を足していきながらつなげていく。例えば上の図だと \[ 1, (3, 4, 2), (6, 7, 8, 9, 5), (11, 12, 13, 10), 14 \] となる。
ただし、 start と goal を入れ替えると辞書順でもっと小さくなる可能性があることには注意する。この場合入れ替えると、 \[ 1, (3, 4, 5, 2), (7, 8, 9, 10, 6), (12, 13, 11), 14 \] となる。両方作ってから比較するのが安全だろう。
ポイント
1WA だったが、最後のミスに気づけたので時間内に AC できた。 2番目までを比べて辞書比較をしてはならない という当たり前のことである。
書き始めた段階で 50 分あったので正解を与える自信はあった。 assert を使って慎重に書いていたので結果的にデバグの時間を節約することができた。
Others
最高レートを更新した。
