AtCoder Regular Contest 058
Updated:
- Review: 2020-07-06
Source codes
Solutions
C - こだわり者いろはちゃん / Iroha’s Obsession
Just try by $n, n + 1, \dots$. Since $n \leq 10 ^ 4$, we can stop before $20000$.
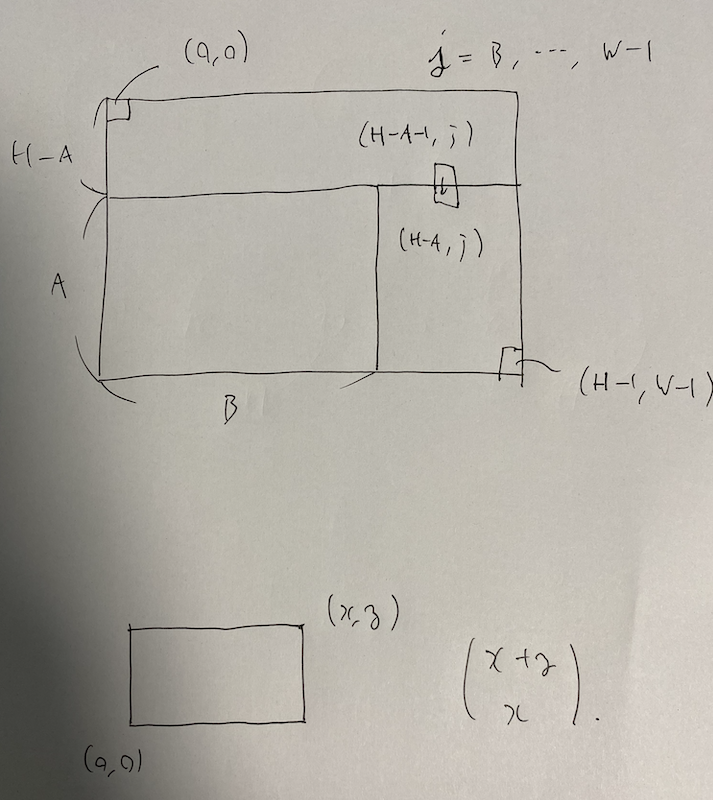
D - いろはちゃんとマス目 / Iroha and a Grid
Every path passes through $(h - a - 1, j) \mapsto (h - a, j)$. This $j \in [b, w)$ is uniquely exists for every path. Thus, the answer is \[ \sum _ {j = b} ^ {w - 1} \begin{pmatrix} (h - a - 1) + j \\ h - a - 1 \end{pmatrix} \begin{pmatrix} (h - 1 - (h - a)) + (w - 1 - j) \\ (h - 1 - (h - a)) \end{pmatrix}. \]
E - 和風いろはちゃん / Iroha and Haiku
Assume $0$-indexed.
How to preserve the last terms
We count the sequence which does not contain any XYZ.
We use bitwise memory. We describe that the previous term is $k$ by 1 << k. For example, we mean that the last $3$ terms are $2, 3, 1$ by $101001 _ {(2)}$. We convert $\{ a _ i \}$ into $bit$ in this way. Then, we see the following properties.
-
Judge of XYZ: We define $haiku = (1 \mathbin{«} (Z - 1)) (1 \mathbin{«} (Z + Y - 1) (1 \mathbin{«} (Z + Y + X - 1)))$, and we determine $bit$ has XYZ if $bit \& haiku = haiku$. - The way of preserving the last terms: We possess $bit \& mask$, where $mask = ((1 \mathbin{«} X + Y + Z - 1) - 1)$. In other words, we save last $X + Y + Z - 1$ bits.
DP part
Definition
vector<vector<mint>>$dp[i][j] = $ the number of the sequences which does not contain any XYZ, where the last terms are described by $j \subset B$.
Initial state
$dp[0][0] = 1$; otherwise $0$.
Answer
\[ 10 ^ n - \sum _ {j \subset mask} dp[n][j]. \]
Transition
For $i = 0, \dots, n - 0$, for $j \subset mask$, we execute as follows. If $dp[i][j] = 0$, continue;. Otherwise, for $k = 1, \dots, 10$, let
\[
nj = (j \mathbin{«} k) | (1 \mathbin{«} (k - 1)).
\]
If $nj$ contains $haiku$, continue;. Otherwise, we execute the following line.
\[
dp[i + 1][nj \& mask] \mathbin{+=} dp[i][j].
\]
